Эффект Холла

Эффект Холла заключается в возникновении разности потенциалов в образце в направлении, перпендикулярном магнитному полю и электрическому току. Это явление, открытое в 1879 г. Холлом, широко применяется для исследования электрических свойств твердого тела, и за последнее время нашло ряд важных применений в технике. Рассмотрим физику этого явления подробнее.

Пусть имеется проводник или полупроводник в форме прямоугольной пластинки, по которой течет электрический ток плотностью j. Эквипотенциальными поверхностями будут плоскости, перпендикулярные к направлению тока, и поэтому разность потенциалов между двумя металлическими зондами 1 и 2 рис. 163, лежащими в одной из этих плоскостей, будет равна нулю. Если в образце создать магнитное поле, перпендикулярное к току и к зондам, то между зондами возникает разность потенциалов. Это значит, что эквипотенциальные поверхности в пластине становятся наклонными. Опытным путем Холл установил, что возникающая разность потенциалов U_1,2 пропорциональна плотности тока j, индукции магнитного поля В и расстоянию между зондами d:

Коэффициент пропорциональности R_x является константой материала и носит название постоянной Холла.

Явление Холла объясняют с точки зрения электронной теории как результат действия силы Лоренца на отдельные свободные носители тока. Так как свободных зарядов внутри твердого тела нет, то привлекать силу Лоренца для объяснения явления Холла не состоятельно. Реально это явление заключается в следующем.

Электрический ток внутри твердого тела представляет собой распространение электромагнитных волн, которые у поверхности проводника создает магнитное поле В´. Это магнитное поле с напряженностью электрического поля волны связаны соотношением (5.22). В отсутствие внешнего магнитного поля напряженность электрического поля электромагнитной волны на поверхностях 1 и 2 не изменяется, а поэтому их разность равна нулю. При наложении внешнего магнитного поля ситуация меняется. На поверхности 1 напряженность поля электромагнитной волны равна

а на плоскости 2

Здесь в соответствии с (8.7) - наведенная магнитная индукция внутри материала, а κm – магнитная восприимчивость используемого материала.

С учетом взаимной перпендикулярности векторов Е, v и В´ разность напряженностей полей равна

Если умножить равенство (13.4) на расстояние d, то левая часть равенства (13.4) даст разность потенциалов U_1,2 и тогда

Такая разность потенциалов возникает только при прохождении электрического тока. Учтем это обстоятельство путем умножения правой части равенства (13.5) на плотность тока и делением на плотность тока. Тогда

Сравнивая (13.6) с (13.1), получим для коэффициента Холла выражение

Отсюда для диамагнетиков κm < 0 и тогда R_x < 0. Для парамагнетиков и ферромагнетиков κm > 0. Поэтому R_x > 0. В качестве примера рассмотрим зависимость коэффициента Холла от температуры для ферромагнетиков никеля и диспрозия, изображенных на рис. 164 (а,б).

Для никеля диполь-дипольная связь внутри кластера несколько больше межкластерного взаимодействия (см. табл.8.2). Поэтому температура Кюри выше температуры Нееля и в диамагнитное состояние никель не переходит, но, вследствие разрыва связи между кластерами, значительно ослаблено наведенное магнитное поле внутри проводника. Коэффициент Холла по прежнему является положи 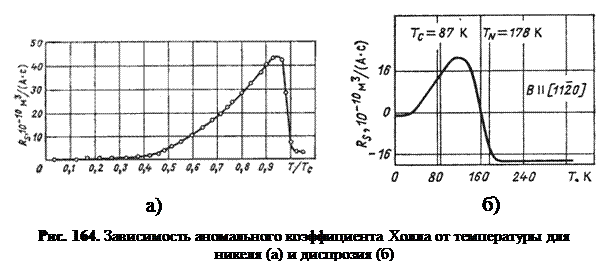тельным.

Для диспрозия температура Кюри меньше температуры Нееля. Когда же температура достигает выше температуры Нееля диполь-дипольное взаимодействие полностью разрушается и вещество переходит в диамагнитное состояние. Коэффициент Холла становится отрицательным.

Коэффициент Холла не является постоянной величиной, а зависит от электрических свойств материала, по которому протекает электрический ток. Зависимость эта прямо пропорциональна скорости распространения электромагнитной волны как по волноводу в проводнике и обратно пропорциональна проводимости данного материала, а также тангенциальной напряженности электрического поля, создаваемой внешним источником тока для электромагнитных волн. Поэтому измерение коэффициента Холла позволяет получать основные свойства твердых тел проводить электрический ток.

Сравнить теоретический расчет с экспериментальными данными не представляется возможным, так как при проведении измерений коэффициента Холла тангенциальная составляющая напряженности электрического тока не контролировалась. В частности, для образцов из чистой меди, чтобы опытные данные совпали с теоретическим расчетом необходимо тангенциальную часть напряженности электрического поля положить равной 2,44∙10^-4 В/м. В подобных экспериментах используются тонкие пластины, для которых омическое сопротивление достаточно мало и поэтому на них приходится малое падение напряжения и, соответственно, реализуется малая тангенциальная напряженность электрического поля, что и подтверждается теоретическим расчетом.

Вблизи абсолютного нуля температуры распределение электронной плотности сосредоточено около уровня Ферми. На уровне Ферми вероятность заполнения свободного энергетического состояния составляет 0,5. Поэтому для диамагнетиков коэффициент Холла увеличивается в два раза. Если учесть, что тангенциальная составляющая несколько изменяется, то результирующее увеличение коэффициента Холла будет около двух, как это было установлено экспериментально. Так для алюминия этот рост составляет ~ 2,8, а для меди ~ 1,5.

Одновременное изменение двух величин, зависящих от приложенного внешнего магнитного поля, приводит к изменению знака коэффициента Холла.

Поиск по сайту: