Резонанс тока в электрических цепях

Резонанс тока возникает в параллельном RLC -контуре, как это показано на рис.120. На вход параллельного RLC -контура подается переменное напряжение с амплитудным значением U₀ и частотой ω. Применим к этой цепи правила Кирхгофа. По первому правилу в точке А замкнутого контура RLC для тока получаем равенство

, (10.54)

а в соответствии со вторым правилом

. (10.55)

В свою очередь при малом омическом сопротивлении (R → 0) получаем:

. (10.56)

В резонансных условиях . Тогда , а на основании (10.54) ток потребления I от источника равен нулю. В соответствии с законом Ома для участка цепи RLC следует полагать, что такая цепь для переменного тока в резонансных условиях представляет собой бесконечное сопротивление. Парадокс! Параллельная RLC -цепь от источника электрическую энергию не потребляет, а внутри такого контура возникают колебания электрического и магнитного поля. Колебания магнитного поля фиксируются как колебания электрического тока. Оценим этот ток.

Решая систему уравнений (10.54) и (10.55), имеем:

, (10.57)

а с учетом определения резонансной частоты ω_рез (10.46), коэффициента затухания β (10.25) и добротности Q (10.27), получаем:

. (10.58)

Из (10.58) следует, что электрические токи внутри параллельного RLC -контура возникают огромной величины по сравнению с величиной электрического тока, потребляемого от источника питания. Это свойство параллельного RLC -контура используется в различных связанных системах, как то: при организации радиосвязи, для создания резонансного трансформатора Николы Тесла, резонансного мотор-генератора и при передаче электроэнергии по одному проводу.

10.5.3. Связанные колебательные LC -контуры

Для первого контура имеем:

Аналогично для второго контура

В результате для двух связанных LC -контуров получаем следующую систему двух дифференциальных уравнений второго порядка:

Умножим второе уравнение на L_1,2/L₁ и вычтем одно из другого. Тогда

или

Запишем полученное уравнение (10.62) в более компактном виде

где

Теперь умножим первое уравнение системы (10.61) на L_2,1/L₂ и вычтем его из второго уравнения, и после проведения аналогичных преобразований, как это было проделано выше для первого случая, получим:

где

Таким образом, необходимо решить два совместных дифференциальных уравнений второго порядка вида:

В установившемся процессе колебания в обоих контурах будут совершаться с одной и той же частотой. Тогда решение первого и второго уравнения можно представить в виде:

где Q_0,1 и Q_0,2 - амплитудные значения зарядов, сосредоточенных в конденсаторах первого и второго LC -контуров.

Найдем вторые производные от выражений (10.66) и подставим их в уравнения (10.65). В результате получим:

или

Получено два уравнения с двумя неизвестными Q_0,1 и Q_0,2, т.е. система линейных однородных уравнений. Отношение амплитуд Q_0,1/Q_0,2 из первого и второго уравнений системы (10.67) равно

В более общем случае и

Тогда частоты колебаний в первом и во втором LC -контурах будут равными, а поэтому и отношение амплитуд окажутся разными для обоих контуров

Рассмотрим случай, когда параметры колебательных контуров одинаковые. В этом предположении α _1,1 = α _2,2 и α _1,2 = α _2,1. Тогда соответственно: С = С₁ = С₂ и L = L₁ = L₂, а также L_1,2 = L_2,1 и Q₀ = Q_0,1 = Q_0,2. Из первого уравнения системы (10.67) следует:

а из второго уравнения

Подставляя полученные значения частот колебаний в соответствующие отношения амплитуд (10.69) получим: h₁ = - 1 и h₂ = 1. Результирующее колебание в первом LC -контуре представляется в виде суперпозиции двух колебаний вида

и аналогично во втором LC -контуре

Получается, что в первом и во втором контурах колебания представляют собой результат сложения колебаний с одинаковыми амплитудами, но с разными частотами. Связь между контурами осуществляет коэффициент взаимной индукции. При сравнительно слабой связи L_1,2 << L получаем:

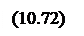
Здесь - собственная частота колебательного контура.

Разность частот | ω₁ - ω₂| = ω₀L_1,2/L составляет малую величину, и совершаются эти колебания в одном направлении. Поэтому результирующее колебание представляет собой явление биения. Частота биений соответствует разности складываемых колебаний и равна

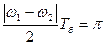
Таким образом, при слабом коэффициенте связи происходит полная перекачка энергии от одного колебательного контура к другому со временем равном периоду биений

Аналогичные преобразования для емкостной связи (рис.121 б) дают следующие частоты

При L₁ = L₂, C₁ = C₂ и C₁ << C частоты ω₁ и ω₂ будут отличаться незначительно и вследствие этого возникнет явление биения. В этом случае период биений равен

В сложных электрических цепях возникают одновременно емкостные и индуктивные связи. Рассмотрение таких сложных связанных систем выходит за рамки настоящего пособия.

Явление биения возникают в радиосвязи, когда частота передатчика или приемника уходят от своей резонансной частоты. Вследствие этого происходит замирание сигнала. Это явление также используется в радиолокации для определения скорости движения цели, по изменению частоты отраженного сигнала от цели вследствие эффекта Доплера.

10.5.4. Резонансный трансформатор Николы Тесла

Общая схема обычного трансформатора показана на рис. 122. Он состоит из двух обмоток – первичной и вторичной, навитых на железный сердечник, нагруженный на сопротивление нагрузки R₂. Уравнение колебаний электромагнитного поля в такой системе в первичной и вторичной обмотках имеют вид:

, (10.76)

где - соответственно изменяющиеся магнитные потоки со временем, которые пронизывают первичную и вторичную обмотки. Пренебрегая рассеянием магнитного потока в обмотках трансформатора, получаем:

. (10.77)

Здесь n₁ и n₂ – соответственно число витков первичной и вторичной обмоток.

В таком трансформаторе возникают потери энергии на преодоления магнитного гистерезиса. Причем, чем большая частота колебаний, тем большие реализуются потери. Чтобы этого избежать Никола Тесла предложил оригинальную схему воздушного резонансного трансформатора, изображенного на рис. 123. В таком трансформаторе отсутствуют потери на преодоление гистерезиса, а для повышения пронизывающего магнитного потока первичной и вторичной обмоток используется резонансный режим.

Первичная обмотка в таком трансформаторе имеет небольшое число витков ленточного типа. Такие витки обладают малой индуктивностью, и одновременно выполняют роль электроемкости. Первичная катушка замкнута на внешнюю электроемкость. Такая система представляет собой параллельный RLC -контур. Параллельный RLC -контур возбуждается от катушки Румкорфа разрядником F. Разрядник F генерирует П-образные импульсы тока с широким спектром частот электромагнитных колебаний. Поэтому резонанс первичной обмотки возбуждается целым спектром резонансных частот (). Дроссели D служат для предохранения катушки Румкорфа от воздействия обратных высокочастотных токов, которые значительно усилены резонансным контуром.

Вторичная обмотка со многими витками тонкой проволоки помещается внутри первичной. Обе обмотки хорошо изолированы друг от друга. Витки в каждой обмотке также хорошо изолированы. Когда пробивается искровой промежуток F, то в первичном контуре возникают высокочастотные электрические колебания. Если эти колебания по частоте совпадают с резонансной частотой вторичной обмотки, то вокруг такого устройства возникает электромагнитное поле напряженностью более миллиона вольт. Физика такого явления пока остается не ясной. Можно только предположить, что такой трансформатор является антенной для приема электромагнитных волн, создаваемых грозами на всем земном шаре. Это огромная энергия и опасная для биосферы нашей планеты.

Никола Тесла не был сторонником электронной теории протекания электрического тока, а считал, что электрический ток представляет собой распространения электромагнитных волн. Поэтому он предложил передавать электромагнитную энергию по одному проводу, а при очень высоких частотах – беспроводную передачу энергии электромагнитного поля. Только в наше время реализована передача энергии электромагнитного поля по одному проводу и беспроводная передача в промышленном масштабе.

10.5.5. Резонансная передача энергии
электромагнитного поля по одному проводу

Однопроводная электрическая система передачи электроэнергии по одному проводу в резонансных условиях осуществляется токами смещения, а по- этому ленцаджоулевы потери на нагрев проводов в линиях передачи незначительные. Общая схема однопроводной электрической системы показана на рис. 124. В качестве линии электропередачи может быть использован любой проводник, который в данном случае является направляющей для потока электромагнитной энергии, передаваемой от генератора к приемнику. Параллельный RLC -контур в начале линии электропередач состоящий из первичной обмотки повышающего высокочастотного резонансного трансформатора и батареи конденсаторов подключен к статическому преобразователю частоты. Аналогичный понижающий резонансный трансформатор размещен в конце линии электропередачи, к выходу которого подключен выпрямитель с соответствующей нагрузкой.

Такая линия электропередачи обеспечивает: уменьшение расхода цветных металлов в 100 раз; снижает расходы на строительство линий электропередач и снижает потери энергии в электросетях. Это можно понять из следующего примера. По однопроводной линии из медного провода длиной 6 м и диаметром 80 мкм передана в непрерывном режиме активная электрическая мощность 20,4 кВт при напряжении 6,8 кВ, при этом эффективные плотности тока и мощности составили соответственно 600 А/мм² и 4 МВт/мм². При подключении такого провода к 50-и герцовой сети провод просто взорвался бы.

Это не единственная реализация резонансных свойств RLC -контура. В настоящее время разработан резонансный генератор с избыточной энергией. Рассмотрим такую систему подробнее.

Поиск по сайту: