Явление самоиндукции

Всякий проводящий замкнутый контур с током всегда находится в магнитном поле, созданном самим током, который протекает в этом контуре. Поэтому при изменении тока в контуре произойдет изменение связанного магнитного потока через поверхность контура, а в самом контуре возникнет ЭДС индукции. Явление возникновения ЭДС индукции в контуре при изменении тока в этом контуре называется явлением самоиндукции.

Магнитное поле, создаваемое проводником с током, можно охарактеризовать некоторым потоком магнитной индукции - потокосцеплением. Потокосцепление пропорционально величине тока i:

, (7.9)

где L - коэффициент пропорциональности, получивший название коэффициента самоиндукции.

За единицу измерения коэффициента самоиндукции принимается 1 генри. Это величина такого контура, в котором при изменении тока 1 А в 1 с возникает ЭДС в 1 В: . (7.10)

С изменением тока во времени происхо­дит изменение потокосцепления, и ЭДС самоиндукции запишется так:

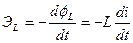. (7.11)

Под влиянием ЭДС самоиндукции при замыкании и размыкании электрической цепи в ней возникают экстратоки. Экстратоки самоиндукции в соответствии с законом Ленца всегда препятствуют изменению тока, вызвавшего их. Рассмотрим это явление подробнее.

Пусть имеется цепь, состоящая из контура L, лампочки Л с резистором R, батареи Б и ключа К (рис. 68).

При замыкании ключа по цепи пойдет ток и возникнет магнитный поток, пронизывающий виток контура L. В соответствии с правилом Ленца магнитный поток индукционного тока будет противодействовать нарастанию магнитного потока основного тока, т.е. будет направлен в противоположную сторону (пунктирные кривые). Индукционный ток (экстраток), таким образом, имеет направление, противоположное направлению основного тока, вследствие чего последний не сразу достигнет величины, определяемой законом Ома: I₀=Э/R, где Э - ЭДС батареи, R - полное сопротивление всей цепи. Лампочка Л будет разгораться постепенно.

Установим характер изменения тока в цепи. Так как в цепи кроме ЭДС источника действует еще ЭДС самоиндукции, то можно записать следующее равенство: . (7.12) Это равенство преобразуем к виду

. (7.13)

Разделим переменные и проинтегрируем правую и левую части:

.

После взятия интеграла окончательно получим:

. (7.14)

Из (7.14) видно, что ток растет по экспоненциальному закону и достигает значения I₀ через бесконечное время. Практически ток i(t) будет отличаться от I₀ на малую величину уже через сравнительно небольшой отрезок времени, равный: t = L/R. Эта величина называется временем релаксации или постоянной времени RL цепи.

Когда t = τ = L/R, показатель степени экспоненты равен единице со знаком «минус» и i = 0,63 I₀. Время релаксации в данном случае есть время, в течение которого ток в цепи достигает значения 0,63 от максимального значения I₀ (рис. 69).

Рассмотрим обратный процесс, когда ток в цепи выключается. Поток, связанный с током витка, полностью исчезает. Изменение магнитного потокосцепления вызывает появление тока самоиндукции (экстратока размыкания), который своим магнитным полем будет поддерживать магнитный поток основного тока. В этом случае ток самоиндукции направлен так же, как и основной. В результате в цепи возникает постепенно убывающий ток и лампочка гаснет не сразу.

Установим закон убывания тока в цепи. Предположим, что в уравнении (7.12) Э = 0. Это условие отключения источника питания. Тогда

или .

Разделим переменные и проинтегрируем:

.

Отсюда 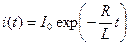. (7.15)

Следовательно, сила тока в цепи убывает по экспоненциальному закону (рис. 70).

Скорость убывания определяется временем релаксации . Чем больше индуктивность и меньше сопротивление, тем медлен­нее происходит исчезновение тока в цепи.

Из выражения (7.11) следует, что разность потенциалов, возникающая в контуре при изменении электрического тока может быть представлена в виде

.

Отсюда ток в цепи в любой момент времени t можно выразить следующим образом:

.

Здесь - начальный ток, определяемый всей предысторией протекания тока в цепи до момента отсчета времени t.

Поиск по сайту: