Колебания электромагнитного поля в LC-контуре

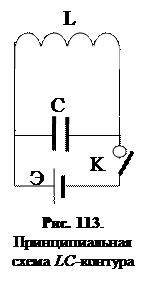Принципиальная электрическая схема LC -контура приведена на рис. 113. От источника ЭДС напряжением U_э ключом К заряжается электроемкость С и затем отключается. Энергия, которая при этом была передана LC- контуру, равна

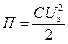. (10.7)

После отключения источника ЭДС электроемкость С начнет разряжаться через индуктивность L. В цепи возникнут электромагнитные колебания и вследствие этого энергия электрического поля, запасенная в электроемкости, будет переходить в энергию магнитного поля, сосредоточенной в индуктивности L. Закон сохранения энергии в этом случае в момент времени t запишется в виде:

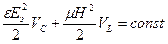. (10.8)

Здесь V_C и V_L – объем, в котором сосредоточено электрическое поле и магнитное поле соответственно. Уравнение (10.8) можно записать иначе, а именно:

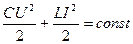. (10.9)

Выразим уравнение (10.9) через электрический заряд, сосредоточенный на обкладках электроемкости. Тогда

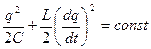. (10.10)

Со временем изменяются как электрическое, так и магнитное поле. Возникнут электрические колебания в идеальном колебательном контуре LC. Покажем, что такие колебания являются гармоническими. Чтобы выяснить закон изменения электрического поля внутри электроемкости или магнитного поля внутри индуктивности возьмем производную от уравнения (10.10) по времени t, ипосле сокращения на dq/dt получаем:

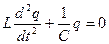
или после сокращения на L 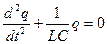. (10.11)

Сравним полученное выражение с уравнением механических гармонических колебаний, в которых потенциальная энергия переходит в кинетическую энергию, вида: 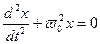. (10.12)

Отсюда следует, что роль смещения от положения равновесия, выполняет заряд q, роль потенциальной энергии выполняет электрическое поле, роль кинетической энергии выполняет – магнитное поле. Используя эту аналогию, частота электрических колебаний в LC -контуре равна

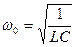, (10.13)

а период колебаний 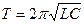. (10.14)

Формула (10.14) носит имя Томсона, которая им впервые была получена.

Решением уравнения (10.11) является функция вида:

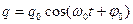. (10.15)

Здесь q₀ – амплитудное значение заряда на обкладках конденсатора; 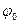- начальная фаза. Разделив уравнение (10.15) на электроемкость и расстояние между обкладками конденсатора, получим:

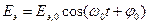. (10.16)

Возьмем производную по времени от выражения (10.15).

Тогда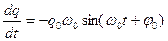

или .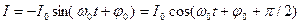

Но электрический ток в катушке индуктивности линейно связан с напряженностью магнитного поля. Поэтому

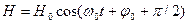. (10.17)

Таким образом, в LC -контуре совершают гармонические колебания напряженность электрического поля внутри конденсатора и напряженность магнитного поля внутри индуктивности с частотой 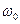. Наличие в электрической цепи электроемкости приводит к тому, что электромагнитная волна при отражении от пластин конденсатора существенно изменяется. Электрическое поле волны отражается от менее плотной среды и поэтому обладает пучностью, а электрический ток не распространяется через конденсатор. Электрический ток на границе раздела металл-окружающая газовая среда равен нулю, и поэтому для магнитной составляющй возникает узел, т.е. электрическое и магнитное поле совершают колебания с разностью фаз π/2. Вследствие этого внутри LC -контура происходит взаимное превращение энергии электрического поля в энергию магнитного поля в соответствии с законом сохранения энергии. Это приводит к тому, что внутри конденсатора возбуждаются электрон-позитронные пары физического вакуума, а внутри индуктивности – магнитная составляющая физического вакуума. Возникает взаимодействие электромагнитных колебаний в LC -контуре со структурой физического вакуума дважды – внутри конденсатора и внутри индуктивности. При этом внутри такой замкнутой цепи создается стоячая электромагнитная волна на частоте собственных колебаний данного контура независимо для электрического и магнитного полей со здвигом фаз π/2. Поэтому и происходит взаимное превращение энергий электрического и магнитного полей, т.е. энергия одной стоячей волны переходит в энергию другой стоячей волны, как это имеет место в различных связанных колебательных системах.

Поиск по сайту: