Закон электромагнитной индукции

Совместно связанные электрическое и магнитное поля описываются уравнением

. (7.1)

Запишем это уравнение в координатной форме (рис.63). Выберем на оси Y элемент 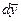в направлении вектора _э и умножим равенство (7.1) скалярно на вектор 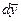. В результате получим такое равенство:

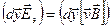(7.2)

Учитывая, что все вектора взаимно перпендикулярны, раскроем скалярное и векторное произведения

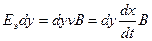. (7.3)

Произведение 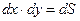есть дифференциал от переменной площади S, а произведение E_эdy в соответствии c (2.5) есть электродвижущая сила 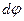. Следовательно, (7.3) запишем в виде:

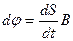или 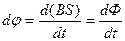. (7.4)

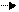
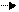Получается, что при изменении магнитного потока должна возникать разность потенциалов вдоль направления, перпендикулярного вектору скорости изменения магнитного потока и вектору магнитной индукции. Представим эту ситуацию на рис. 64. Пусть проводник длиной l движется в магнитном поле со скоростью v перпендикулярно силовым линиям магнитного поля, и за время t прошел расстояние x. Тогда перпендикулярно векторам v и B возникает напряженность электрического поля, которая направлена вдоль проводника. Под влиянием внешнего поля внутри проводника возникнет поляризация среды и на это будет затрачена работа. Физически этот процесс представится так:

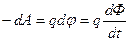или 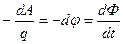. (7.5)

Запишем равенство (7.5) в более удобном виде, а именно:

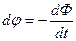. (7.6)

В интегральной форме равенство (7.6) приобретает вид:

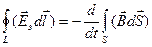. (7.7)

Равенство (7.6) в дифференциальной форме и это же равенство в интегральной форме (7.7) являются математической записью закона электромагнитной индукции. Первое равенство относится к элементу проводника, а второе равенство – к замкнутому контуру.

Экспериментально знак минус в формулах (7.6) и (7.7) был установлен профессором Петербургского университета Ленцем в 1833 г. Обобщая результаты опытов, он сформулировал следующее правило: возникающий в замкнутом контуре вследствие изменения магнитного потока индуцированный ток имеет такое направление, что уменьшает своим магнитным полем изменение магнитного потока, которое вызвало этот ток.

Возникновение разности потенциалов на концах проводника, когда он пересекает магнитное поле, имеет принципиальное значение и впервые исследовано Фарадеем.

В конце 1821 г. в дневнике Фарадея была сделана запись: «Превратить магнетизм в электричество», а в августе 1831 г. получен первый результат.

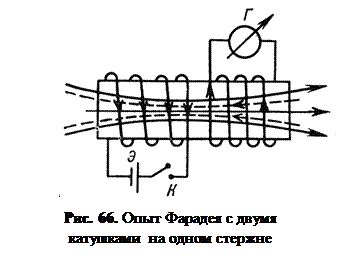
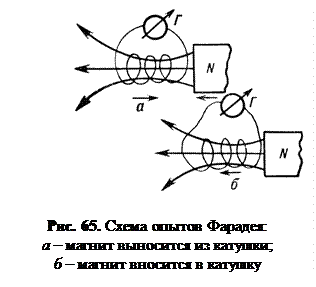
Опишем опыты Фарадея. Если внести магнит в соленоид, а его концы подключить к гальванометру Г (рис. 65 а), то последний покажет наличие тока в соленоиде. Аналогичная ситуация возникает, если вытягивать магнит из соленоида (рис. 65 б). Можно опыт видоизменить: на одном стержне разместить две катушки (рис. 66). При включении или размыкании тока ключом К в одной из катушек в другой возникает ток, направление которого таково, что своим магнитным полем он препятствует изменению магнитного поля, создаваемого первой катушкой. Этот же эффект может возникнуть, когда усиливается или ослабляется электрический ток в одной из катушек. Если двигать проводник, замкнутый на гальванометр, в магнитном поле, то в нем возникнет электрический ток такого направления, что своим действием он будет препятствовать первоначальному движению проводника (рис. 67).

В описанных явлениях, несмотря на их многообразие, наблюдается общее: если проводник в виде контура пересекается манитным потоком или проводник пересекает линии магнитного поля, то в случае разомкнутой цепи на концах проводника возникает ЭДС, а в случае замкнутой цепи в ней протекает индукционный ток. Это явление получило название электромагнитной индукции.

Явление электромагнитной индукции заключается в возникновении ЭДС в проводнике, пересекающем силовые линии магнитного поля, или в замкнутом контуре при изменении пронизывающего его магнитного потока. В соответствии с этим можно дать две формулировки закона электромагнитной индукции: первая относится к отрезку проводника; вторая — к замкнутому контуру. Первая представляет формулировку Фарадея или дифференциальную форму закона электромагнитной индукции, так как ее можно применить к сколь угодно малому элементу контура; вторая — формулировку Максвелла или интегральную форму закона.

Формулировка Фарадея: при пересечении потока магнитной индукции отрезком проводника в нем возникает ЭДС электромагнитной индукции, прямо пропорциональная скорости изменения величины магнитного потока, который пересекает проводник при своем движении.

Формулировка Максвелла: при изменении потока магнитной индукции, «сцепленного» с замкнутым проводящим контуром, в последнем возникает ЭДС электромагнитной индукции, прямо пропорциональная скорости изменения магнитного потока.

Математически на основании (7.6) этот закон в самом общем виде можно записать так:

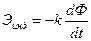(7.8)

В системе СИ k = 1и тогда (7.8) переходит в (7.6).

Поиск по сайту: