Изменение сопротивления в магнитном поле

У всех металлов и полупроводников, кроме ферромагнетиков, удельное сопротивление ρ возрастает при включении магнитного поля. При комнатных температурах для различных металлов и хорошо проводящих полупроводников при протекании электрического тока возникают магнитные поля Н´~ 8∙10⁶ - 8∙10⁷ А/м, а для плохо проводящих полупроводников - Н^´ ~ 8∙10⁸ - 8∙10⁹ А/м. В обычных для физического эксперимента полях Н^´ < 8∙10⁵ А/м при комнатных температурах изменение удельного сопротивления ∆ρ/ρ большинства металлов крайне незначительно. Так, у меди при Н = 2,4∙10⁶ А/м ∆ρ/ρ ~ 10^-4. Исключение составляет висмут, у которого при Н = 1,6∙10⁶ А/м ∆ρ/ρ ~ 200%. Это используется для измерения магнитных полей. У полупроводников ∆ρ/ρ может составлять ~ 1. Так, у германия при температуре 90 К и Н = 4∙10⁶ А/м ∆ρ/ρ ~ 10^-4. Исключение составляет висмут, у которого при Н = 1,46∙10⁶ А/м ∆ρ/ρ = 300%.

Впервые существенное изменение сопротивления проводящих кристаллов под действием внешнего магнитного поля было получено П.Л. Капицей в 1927 г. (в будущем лауреат Нобелевской премии), который использовал импульсные магнитные поля в 10⁷ и 10⁸ А/м. В этом случае ∆ρ/ρ для металлов составляло несколько десятков процентов.

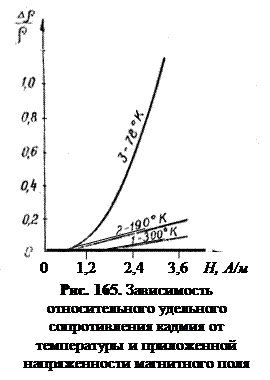
На рис. 165 в качестве примера приведены изотермы относительного изменения сопротивления кадмия (Cd) в поперечном магнитном поле, полученные П.Л. Капицей. Анализ экспериментальных кривых показывает, что при сравнительно малых полях, создаваемых электрическим током ∆ρ/ρ ~ Н², а при сильных полях ∆ρ/ρ ~ Н. особенно сильно эффект возрастания удельного сопротивления сказывается при низких температурах.

Обычно предполагалось, что действие магнитного поля сводится к тому, что траектория свободных электрических зарядов носителей тока искривляется, и направление их движения отклоняется от первоначального на некоторый угол. Вследствие этого на основании электронной теории Друде-Лоренца электросопротивление растет на величину изменения длины свободного пробега. В этой связи при слабых внешних магнитных полях электрическое сопротивление растет пропорционально квадрату напряженности приложенного магнитного поля, а при сильных внешних магнитных полях электрическое сопротивление растет линейно от приложенной напряженности внешнего магнитного поля.

На основании представлений о движении электронов в проводнике, предполагающих одинаковую скорость и одинаковую длину свободного пробега у всех электронов, ни поперечное, ни тем более продольное внешнее магнитное поле не должно приводить к изменению электрического сопротивления исследуемого кристалла того или иного металла. Поперечное к электрическому полю ускорение, вызванное магнитным полем, полностью компенсируется электрическим полем эффекта Холла, и, следовательно, пути электронов остаются не искаженными магнитным полем, а электросопротивление – неизменным. Привлечение анизотропии свойств кристаллов и максвелловский разброс скоростей существенно ничего не изменит. Рассмотрим эффект изменения электрического сопротивления во внешних магнитных полях с точки зрения распространения электромагнитных волн, которые создают электрический ток.

Учитывая равенство по абсолютной величине нормальной и тангенциальной составляющих электрического поля при протекании электрического тока, на внешней поверхности 1 (см. рис.163) Е_n - Е_х = Е_τ - ∆ Е_τ, а для поверхности 2 Е_n + Е_х = Е_τ + ∆ Е_τ. Как из первого равенства, так и из второго следует, что изменение тангенциальной напряженности электрического поля равно напряженности поля Холла:

∆ Е_τ = Е_х.

Для изменения поглощенной энергии проводником в соответствии с вектором Умова-Пойнтинга и законом Ома получаем:

Здесь S = bd – сечение исследуемого кристалла.

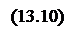
На основании (13.9) с учетом (13.4) изменение электрического сопротивления равно

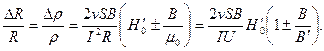
Поделим (13.10) на электрическое сопротивление проводника и учтем закон Ома

При В << B´ реализуется линейная зависимость относительного изменения сопротивления от внешнего приложенного магнитного поля В, т.е.

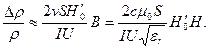
При В >> В´ возникает квадратичная зависимость относительного изменения удельного сопротивления от внешнего приложенного магнитного поля. На основании (13.11)

Чем больше удельное сопротивление, тем выше общее сопротивление проводника. Электрический ток при заданном внешнем приложенном напряжении меньше и, соответственно, меньше магнитная индукция В´. В этом случае квадратичная зависимость будет сказываться при меньшем значении внешнего приложенного магнитного поля В.

Так как в проводниках относительная диэлектрическая проницаемость по экспоненте уменьшается с ростом температуры (см. 3.15), то относительное удельное сопротивление также резко уменьшается с температурой, что и подтверждается на опыте (см. рис.164). При малых температурах энергия ионизации кластера (~ 1 эВ) сдерживает заметное изменение относительной диэлектрической проницаемости проводника, и поэтому увеличение удельного сопротивления обусловлено в основном влиянием приложенного магнитного поля. В этом случае реализуется резкая квадратичная зависимость от напряженности магнитного поля. Конкретные расчеты экспериментальных данных произвести не представляется возможным, так как неизвестно какие были использованы падения напряжения на исследуемых проводниках и какие при этом были реализованы электрические токи. Например, для медного проводника на основании (13.12) имеем:

При Н = 2,4∙10⁶ А/м и U = 1 В ∆ρ/ρ ~ 2,7∙10^-2, а при U = 100 В получаем ∆ρ/ρ ~ 10^-4 как это было получено экспериментально.

С позиций протекания электрического тока по проводникам вследствие распространения электромагнитных волн рассмотрим термомагнитные явления.

Поиск по сайту: