Магнитные свойства изолированного aтoмa

Грубо можно представить, что электрон в атоме движется по круговой орбите. В результате этого электрон обладает механическим моментом относительно ядра атома, а круговой ток, который он создает, обусловливает магнитный момент электрона. Оба момента должны быть как-то связаны между собой. Механический момент материальной точки (электрона) массой т_е, если она равномерно вращается по окружности радиуса r, будет равен:

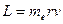. ( 8.10 )

Магнитный момент 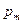той же орбиты равен произведению кругового тока на площадь, которую он охватывает. За единицу времени электрон через определенную точку на орбите пройдет раз. Поэтому ток равен:

,

а магнитный момент - 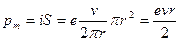. (8.11)

Если электрон движется против часовой стрелки, то вектор 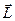направлен вверх, а вниз (рис. 80). Отношение 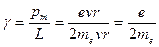не зависит от размера орбиты и определяется только универсальными постоянными. Величина 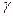называется гиромагнитным отношением. Таким образом, орбитальный магнитный момент атома линейно связан с механическим моментом кругового тока

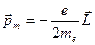. (8.12)

При выводе формулы (8.12) использовалась обычная классическая механика. Однако эти же соотношения справедливы и в квантовой механике.

Атом обладает магнетизмом не только в результате наличия орбитального движения. Электрон обладает еще и спином, которому тоже присущи магнитный и механический моменты. Чисто квантовомеханическое рассмотрение дает, что

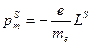. (8.13)

Классическое объяснение этому совершенно отсутствует. В любом атоме имеется несколько электронов, и его полный механический момент и полный магнитный момент представляют некоторую комбинацию спиновых и орбитальных моментов. В квантовой механике для изолированного атома направление магнитного момента всегда противоположно направлению момента импульса. Отношение их не обязательно должно быть 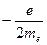или 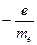; оно может иметь промежуточное значение, ибо здесь «перемешиваются» вклады от спинов и орбит. В общем случае

,

где множитель g носит название фактора Ланде. Для чисто орбитальных моментов он равен единице, для чисто спиновых - двум, а для сложной атомной системы - принимает значения от 1 до 2.

В ядре атома протоны и нейтроны движутся по своего рода орбитам и в то же время, подобно электронам, имеют спин. Магнитный момент параллелен моменту импульса, и поэтому для протона, который равномерно вращается по окружности, имеем:

.

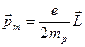В целом для ядра

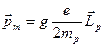, ( 8.14 )

где постоянная g называется ядерным g -фактором, который определяется отдельно для каждого сорта ядерных частиц.

8.4. Атом во внешнем магнитном поле

Теория диамагнетизма. Атом, обладающий магнитным моментом 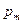, при помещении во внешнее магнитное поле будет испытывать со стороны поля действие момента силы:

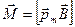. (8.15)

В результате атом развернется в магнитном поле так, что его магнитный момент совпадет с направлением магнитного поля. Но атомный магнит - это миниатюрный гироскоп, у которого имеется момент импульса 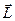. Поэтому вместо разворота атом во внешнем магнитном поле начнет прецессировать (рис. 81) с некоторой угловой скоростью 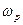вокруг оси, параллельной магнитному полю. Предположим, что за малый промежуток времени 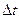момент импульса меняется от до , оставаясь всегда под одним и тем же углом 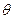к направлению магнитного поля 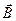. За время 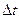угол прецессии приобретает значение . Тогда . Отсюда 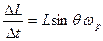и равно моменту силы М. Значит,

.

Откуда 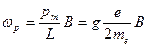. (8.16)

Для атома (или электрона)

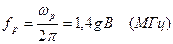
и для ядра

.

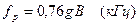То или иное поведение атомов и их ядер во внешнем магнитном поле неизбежно определяет отклик этого вещества на такое внешнее воздействие и приводит к ослаблению или увеличению магнитного поля внутри вещества.

8.5. Диамагнетизм и парамагнетизм
на атомно-молекулярном уровне

Разнообразие типов магнетиков определяется различиями магнитных свойств атомных частиц, образующих вещество данного типа, и характером взаимодействия между ними. Различают электронный и ядерный магнетизм вещества, каждый из которых подразделяется в свою очередь на спиновый и орбитальный. При переходе от отдельных микрочастиц к их соединениям - атомным ядрам, электронным оболочкам атомов и молекул, а затем к их совокупности - газам, жидкостям и кристаллам - все большую роль начинает играть взаимодействие между элементарными носителями магнетизма.

Так, переходя от элемента к элементу в таблице Менделеева, можно наблюдать самые различные случаи магнетизма. Например, электронные оболочки атомов инертных газов магнитно нейтральны. Их результирующие спиновые и орбитальные магнитные моменты равны нулю. Электронная оболочка атомов щелочных металлов обладает лишь спиновым моментом валентного электрона (орбитальный момент у них равен нулю). У атомов с достраивающимися d- и f -оболочками наблюдаются большие спиновые и орбитальные магнитные моменты.

Еще большее разнообразие магнитных свойств реализуется у молекул, а тем более у жидкостей и кристаллов. Сильная зависимость магнитных свойств вещества от характера взаимодействия между микрочастицами приводит к тому, что одно и то же вещество неизменного химического состава при различных температурах, давлении, кристаллической или фазовой структуре может находиться в различных магнитных состояниях. Различают следующие типы магнитных состояний: диамагнетизм, парамагнетизм, антиферромагнетизм, ферримагнетизм и ферромагнетизм. Рассмотрим их подробнее, начиная с отдельных атомных частиц

Диамагнитный момент атома. С классической точки зрения атом можно представить как систему электронов, движущихся вокруг ядра по определенным замкнутым траекториям - орбитам. Для простоты предполагается, что по орбите движется один электрон, который и создает магнитный момент атома. Если на атом накладывается медленно меняющееся магнитное поле, то угловая скорость вращения электрона должна изменяться, а радиус орбиты при этом остается неизменным. Изменение угловой скорости приводит к возникновению некоторого дополнительного механического и магнитного момента атома, который и называется диамагнитным моментом. Рассмотрим возникновение диамагнитного момента атома подробнее,

Известно, что переменное магнитное поле создает вихревое электрическое поле. В соответствии с законом электромагнитной индукции Фарадея

.

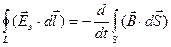Роль замкнутого контура выполняет окружность радиуса r, центр которой совпадает с центром атома (рис. 82). Среднее тангенциальное электрическое поле Е_τ на этом контуре определится выражением

.

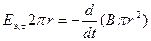Откуда

.

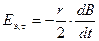Это индуцированное электрическое поле, действуя на атомный электрон, создает момент силы, равный:

В результате имеем: .

Дополнительный момент импульса атома при изме­нении магнитного поля от нуля до В равен: .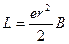

Такой добавочный момент импульса приводит к добавочному магнитному моменту, равному:

. (8.17)

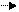Знак «-» в соответствии с правилом Ленца означает, что направление добавочного момента противоположно магнитному полю. Сюда входит квадрат радиуса, который представляет собой расстояние от оси, проходящей через атом и параллельной полю В. В общем случае, поскольку атом обладает сферической симметрией, истинное радиальное расстояние от центра атома (< r² > = x² + y² + z²) составит . Следовательно,

. (8.18)

Величина < r² > находится для каждого атома квантовомеханически.

Таким образом, индуцированный магнитный момент атома пропорционален магнитному полю В ипротивоположен ему по направлению. Поэтому магнитная восприимчивость -- величина отрицательная и индукция 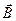в диамагнитном материале уменьшается по сравнению с ее значением в вакууме. Однако этот эффект очень слаб и величина 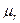лишь незначительно меньше единицы.

К числу наиболее интересных диамагнетиков относятся сверхпроводники. Они обладают бесконечно большой диамагнитной восприимчивостью. Это свойство сверхпроводников используется при конструировании сверхпроводящих магнитов.

Для диамагнитных веществ характерно, что магнитная восприимчивость не зависит от напряженности магнитного поля и от температуры.

Парамагнетизм. Некоторые атомы и ионы обладают постоянными магнитными моментами. В отсутствие магнитного поля моменты обычно ориентированы хаотически по всем направлениям, и микроскопическая намагниченность отсутствует. Однако при наличии магнитного поля эти моменты стремятся ориентироваться преимущественно в направлении поля. Когда магнитные моменты отдельных атомов и ионов ориентируются под действием поля независимо друг от друга, то для таких веществ магнитная восприимчивость больше нуля. Вещество, обладающее такими свойствами, называется парамагнитным. В нем магнитная индукция возрастает незначительно по сравнению с ее значением в вакууме.

Для парамагнитных веществ магнитная восприимчивость зависит от природы самих магнитных моментов атомов и от температуры. Ясно, что от Т зависит обратно пропорционально. Эта зависимость была получена Кюри и поэтому носит название закон Кюри.

Поиск по сайту: