 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Ферромагнетики
|
Читайте также: |
Ферромагнетизм обусловлен возможной ориентацией постоянных магнитных моментов целых групп атомов в одном направлении. В результате такие вещества обладают постоянной намагниченностью даже в отсутствие внешнего магнитного поля. К ферромагнетикам относятся элементы в твердом кристаллическом состоянии, такие, как: 1) переходные элементы группы железа с недостроенной, 3 d -оболочкой атома (Fe, Со, Ni); 2) редкоземельные элементы с достраивающейся 4 f -оболочкой (Gd, Tb, Dy); 3) бинарные и более сложные сплавы и соединения этих элементов между собой и с другими неферромагнитными материалами (магнитные сплавы); 4) сплавы и соединения Сr и Мn с неферромагпитными элементами (гейслёровы сплавы). Относительно магнитных свойств этих элементов удалось получить множество экспериментальных данных, которые могут служить основой для понимания явления ферромагнетизма.





 Магнитный гистерезис. Характерной особенностью ферромагнетизма является сложная нелинейная зависимость магнитной индукции внутри вещества от напряженности внешнего магнитного поля. Для некоторых материалов эта зависимость показана на рис. 84. Характерно, что в процессе намагничивания индукция В вначале резко возрастает, а затем замедляется и достигает насыщения. Магнитная восприимчивость
Магнитный гистерезис. Характерной особенностью ферромагнетизма является сложная нелинейная зависимость магнитной индукции внутри вещества от напряженности внешнего магнитного поля. Для некоторых материалов эта зависимость показана на рис. 84. Характерно, что в процессе намагничивания индукция В вначале резко возрастает, а затем замедляется и достигает насыщения. Магнитная восприимчивость  ферромагнетиков может достигать значений 80 - 800 Тл/(А/м). Намагниченность ведет себя в поле Н так же, как и магнитная индукция (рис. 85). В общем случае
ферромагнетиков может достигать значений 80 - 800 Тл/(А/м). Намагниченность ведет себя в поле Н так же, как и магнитная индукция (рис. 85). В общем случае  . Магнитная восприимчивость
. Магнитная восприимчивость  при некотором значении поля Н достигает максимума и при больших полях асимптотически стремится к нулю (рис. 85). Все ферромагнетики в магнитном отношении являются анизотропными, т.е. намагниченность ферромагнитного кристалла изменяется в различных кристаллографических направлениях. Анизотропия нарушается для мелкокристаллических структур.
при некотором значении поля Н достигает максимума и при больших полях асимптотически стремится к нулю (рис. 85). Все ферромагнетики в магнитном отношении являются анизотропными, т.е. намагниченность ферромагнитного кристалла изменяется в различных кристаллографических направлениях. Анизотропия нарушается для мелкокристаллических структур.



 При наложении внешнего магнитного поля Н на ферромагнетик, который находился в размагниченном состоянии, происходит его намагничивание, достигающее при некотором значении поля H насыщения (рис. 86, кривая 1). Произведя намагничивание образца, будем уменьшать магнитное поле H. Намагниченность при этом будет изменяться необратимо: при заданном значении H величина J будет больше, чем на кривой 1. При H = 0 ферромагнетик обладает остаточной намагниченностью JR, для уничтожения которой необходимо приложить поле обратного знака (- Hc). Это поле носит название коэрцитивной силы. Дальнейшее увеличение поля обратного знака до - Hm приводит к намагниченности – JS. При изменении поля от – Hm до + Hm процесс повторяется, но по другому пути (кривая 3, рис. 86). Таким образом, при циклическом изменении магнитного поля Н намагниченность J описывает так называемую петлю гис
При наложении внешнего магнитного поля Н на ферромагнетик, который находился в размагниченном состоянии, происходит его намагничивание, достигающее при некотором значении поля H насыщения (рис. 86, кривая 1). Произведя намагничивание образца, будем уменьшать магнитное поле H. Намагниченность при этом будет изменяться необратимо: при заданном значении H величина J будет больше, чем на кривой 1. При H = 0 ферромагнетик обладает остаточной намагниченностью JR, для уничтожения которой необходимо приложить поле обратного знака (- Hc). Это поле носит название коэрцитивной силы. Дальнейшее увеличение поля обратного знака до - Hm приводит к намагниченности – JS. При изменении поля от – Hm до + Hm процесс повторяется, но по другому пути (кривая 3, рис. 86). Таким образом, при циклическом изменении магнитного поля Н намагниченность J описывает так называемую петлю гис  терезиса. Площадь петли гистерезиса
терезиса. Площадь петли гистерезиса  равна работе, совершаемой полем Н в единице объема ферромагнетика:
равна работе, совершаемой полем Н в единице объема ферромагнетика: 
 , [ Дж/м3 ]. (8.23)
, [ Дж/м3 ]. (8.23)
Энергия, затраченная на перемагничивание ферромагнетика, переходит в тепло. Следовательно, при циклическом перемагничивании происходит разогрев ферромагнетика не только за счет вихревых токов, но и за счет потерь энергии на магнитный гистерезис.
 Площадь и форма петли гистерезиса существенно зависят от температуры, внешних упругих напряжений, термической и механической обработки и т. п. По величине коэрцитивной силы магнитные материалы принято делить на магнитожесткие и магнитомягкие. Для первых Hc достигает 8∙103 - 8∙104 A/м, а для вторых – 0,8 - 0,08 А/м.
Площадь и форма петли гистерезиса существенно зависят от температуры, внешних упругих напряжений, термической и механической обработки и т. п. По величине коэрцитивной силы магнитные материалы принято делить на магнитожесткие и магнитомягкие. Для первых Hc достигает 8∙103 - 8∙104 A/м, а для вторых – 0,8 - 0,08 А/м.
Природа ферромагнетизма. Необходимый признак ферромагнетизма -наличие постоянных магнитныхмоментов электронных оболочеку атомов, из которых состоит вещество. При конденсации магнитоактивныхатомов в кристалл их электронные оболочки частопретерпевают такую деформацию, что кристалл уже не обладает в своих узлах постоянными магнитными моментами. Наибольшей деформации подвергаетсявалентный слой электронной оболочки. Волновыефункции валентны х электронову соседних атомов в кристалле сильно перекрываются, происходит как бы их обобщение. Если атомы, из которых построен кристалл, не относятся к переходным элементам, то решетка ионных остовов в соответствии с принципом Паули имеет замкнутый характер и обладает диамагнитными свойствами.
Существует несколько теоретических моделей для объяснения ферромагнетизма. Первая модель была предложена Гейзенбергом и предполагает, что магнитные моменты локализованы на отдельных атомах. Модель Френкеля-Стонера исходит из коллективизированных электронов. В основе модели Шубина-Вонсовского-Зинера лежит s-d(f) -обмен валентных электронов. Каждая из этих моделей позволяет понять отдельные ферромагнитные свойства того или иного типа кристалла, но не может вскрыть полностью природу ферромагнетизма во всех типах кристаллов. Наиболее плодотворной оказалась третья модель, которая позволила правильно описать магнитные свойства на атомарном уровне. Магнитные свойства конденсированного состояния эта теория в полном объеме объяснить не смогла.
Образование встроенных дипольных электрических моментов у атомов с достраивающимися d - и f -оболочками. Атомы с достраивающейся d -оболочкой являются железо, кобальт, никель, хром, марганец. Во всех этих элементах внешняя s -оболочка, кроме атома хрома, является замкнутой, а d -оболочка – достраивающаяся. Исходные данные указанных атомов приведены в табл. 8.1.
Таблица 8.1.
Потенциалы ионизации (эВ), радиусы электронов (Å), эффективный заряд первой, второй и третьей кратности ионизации, встроенный магнитный момент (А·м2) и встроенный дипольный электрический момент (D, в дебаях)
| Эле-мент | Параметры | ||||||||||
| Θi,1 | Θi,2 | Θi,3 | r1 | r2 | r3 | Z1 ٭ | Z ٭2 | Z3 ٭ | pm·1023 | рэ, | |
| Fe | 7,87 | 16,2 | 30,6 | 1,72 | 1,57 | 1,29 | 0,94 | 1,76 | 2,74 | 2,29 | 2,36 |
| Ni | 7,63 | 18,2 | 35,2 | 1,62 | 1,49 | 1,25 | 0,86 | 1,88 | 3,o4 | 2,12 | 2,44 |
| Dy | 5,94 | 11,7 | 22,8 | 1,77 | 1,67 | 0,90 | 0,73 | 1,35 | 1,43 | 3,79 | 0,349 |
Средние удаления от ядра атомов указанных выше веществ электронов s -состояния и d -состояния разные, но их волновые функции взаимно перекрываются. Вследствие этого происходит гибридизация волновых функций s - и d -состояний. Результирующая волновая функция является суперпозицией волновых функций этих состояний. С учетом нормировки получаем:
 , (8.24)
, (8.24)
где  и
и 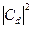 - соответственно вероятности обнаружить оба электрона в s - и d- состояниях. Эти вероятности можно определить, зная времена обращения электронов в s - и d -состояний, а именно:
- соответственно вероятности обнаружить оба электрона в s - и d- состояниях. Эти вероятности можно определить, зная времена обращения электронов в s - и d -состояний, а именно:
 (8.25)
(8.25)
Так как необходимо знать вероятность одновременного пребывания электронов в s- и d -состоянии, то это должна быть совместная вероятность. При этом необходимо учесть вероятность перехода из s- состояния в d -состояние и наоборот. Такая вероятность определяется интегралом перекрытия, вычисленного для одного силового центра
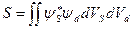 , (8.26)
, (8.26)
где dVs и dVd – элементы объема конфигурационного пространства s и d -состояний.
Среднее удаление между электронами s - и d -состояний соответствует радиусу внешнего валентного электрона в s- состоянии. Следовательно,

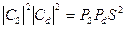 . (8.27)
. (8.27)
Если использовать эффективное главное квантовое число и эффективный заряд с привязкой к потенциалу ионизации водорода, то волновые функции s- и d -состояний можно представить в виде:
 . (8.28)
. (8.28)
Здесь  ,
,
где EH,, ES,, Ed - соответственно энергия ионизации атома водорода и исследуемого атома в s - и d -состояниях.
 Волновая функция (8.24) является гибридной. Гибридизация волновых функций приводит к взаимному смещению относительно ядра атома сферически симметричных s- и d- состояний. В результате возникает внутри атома встроенный дипольный электрический момент. На рис. 87 приведена схема расположения валентных электронов в заданной оболочке в разных энергетических состояниях. Приравнивая центростремительную силу, обусловленную законом Кулона, центробежной силе для обоих электронов с учетом их взаимного отталкивания получаем следующее значение квадрата смещения
Волновая функция (8.24) является гибридной. Гибридизация волновых функций приводит к взаимному смещению относительно ядра атома сферически симметричных s- и d- состояний. В результате возникает внутри атома встроенный дипольный электрический момент. На рис. 87 приведена схема расположения валентных электронов в заданной оболочке в разных энергетических состояниях. Приравнивая центростремительную силу, обусловленную законом Кулона, центробежной силе для обоих электронов с учетом их взаимного отталкивания получаем следующее значение квадрата смещения


Полученное значение усредним по всему объему конфигурационного пространства электронного облака первого и второго электронов, а именно


Биполярный интеграл для одного силового центра равен 96π2α3β3(1/α4β2 + 1/α2β4).
Учтывая только перекрестное взаимодействие, получаем:


В соответствии с (8.31)) встроенный электрический дипольный момент изолированного атома равен
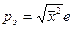 . (8.32)
. (8.32)
Полученные значения электрических диполей по (8.32) различных веществ приведены в табл. 8.1. Полученные значения электрических диполей, для атомов с достраивающейся d -оболочкой, достаточно хорошо коррелируют с аналогичными расчетами, выполненными Коулсоном и другими методами.
Аналогичные расчеты были выполнены для атома диспрозия, у которого взаимодействие возникает между f-s электронами.
Полученным значениям встроенного дипольного электрического момента соответствует встроенный магнитный момент, определяемый по формуле
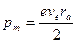 , (8.33)
, (8.33)
где  - скорость валентного электрона первой кратности ионизации на стационарной орбите, rа – радиус нейтрального атома. Результаты вычислений по (8.33) приведены в табл. 8.1.
- скорость валентного электрона первой кратности ионизации на стационарной орбите, rа – радиус нейтрального атома. Результаты вычислений по (8.33) приведены в табл. 8.1.
С учетом наличия в атомах встроенного дипольного электрического момента сравнительно большой величины вследствие гибридизации состояний электронов s- d(f) состояний уточним структуру и энергию связи атомов в кластерах различных веществ.
Образование кластерных структур. Ковалентная связь вычислялась по формуле, которая получена в рамках разработки двухчастичной квантовой механики твердого тела
 , (8.34)
, (8.34)
Здесь суммирование ведется по первой, второй и третьей кратностям ионизации с учетом распределения плотности валентных электронов по энергиям и выполнения расчетов с разными эффективными главными квантовыми числами в процессе вычислений кулоновского (H1,1) обменного (H1,2) интегралов, а также интеграла перекрытия (S); Ni – количество частиц в i -м координационном слое и κ – коэффициент видности, который определен для различных кристаллических структур.
Доля ионной связи определялась по формуле


где Р – суммарная вероятность пребывания одновременно двух валентных электронов вблизи обоих взаимодействующих атомов, R – расстояние между взаимодействующими атомами.

 Каждый валентный электрон взаимодействует со встроенным электрическим диполем противоположного атома. Этот вид взаимодействия оценивался по формуле:
Каждый валентный электрон взаимодействует со встроенным электрическим диполем противоположного атома. Этот вид взаимодействия оценивался по формуле:
Выражение (8.36) выполняется для свободных атомных систем. Если системы связаны не сферически симметричным взаимодействием как это имеет место для ковалентной и ионной связям, а определенным распределением в пространстве, как это реализуется для диполь-дипольного взаимодействия, то формула (8.36) преобразуется к виду
 2), (8.36а)
2), (8.36а)
где  ,
,
а 
функция распределения Максвелла-Больцмана по энергиям.
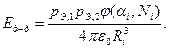 Диполь-дипольное взаимодействие определялось с учетом структуры конденсированной фазы, а именно
Диполь-дипольное взаимодействие определялось с учетом структуры конденсированной фазы, а именно

Здесь φ(αi,Ni) –множитель, определяемый структурой кристалла.
Выполненные расчеты для атомов различных веществ по (8.34)-(8.37) приведены в табл. 8.2.
Таблица 8.2
Энергия бинарной связи различных типов взаимодействия атомов внутри кластера и между кластерами в эВ.
| Тип и энергия взаимодействия | Вещество | |||||||
| Fe | Co | Ni | Cr | Ti | Mn | Gd | ||
| Внутри клас-терное | Еков | 0,380 | 0,388 | 0,432 | 0,505 | 0,255 | 0,355 | 0,054 |
| Еион | 0,136 | 0,144 | 0,178 | 0,172 | 0,091 | 0,203 | 0,010 | |
| Ее-д | 0,5*Wc | 0,5*Wc | 0,6*Wc | 0,4*Wc | 0,4*Wc | 0,5W | 0,5*W | |
| Ед-д | 0,090 | 0,126 | 0,057 | 0,044 | 0,079 | 0,205 | 0,024 | |
| Ерез | 0,606 | 0,635 | 0,667 | 0,721 | 0,425 | 0,763 | 0,089 | |
| Меж- класс- терное | Еков | 0,100 | 0,101 | 0,111 | 0,112 | 0,057 | 0,075 | 0,0054 |
| Еион | 0,004 | 0,003 | 0,003 | 0,004 | 0,0030 | 0,001 | 6·10-5 | |
| Ее-д | 0,3*Wc | 0,1*Wc | 0,2*Wc | 0,049*W | 0,05*W | 0,5W | 0,04W | |
| Ед-д | 0,109 | 0,156 | 0,040 | 0,062 | 0,098 | 0,114 | 0,024 | |
| Ерез | 0,213 | 0,258 | 0,162 | 0,167 | 0,161 | 0,190 | 0,079 | |
| Потенциал ионизации кластера, В | 1,46 | 1,44 | 1,39 | 1,25 | 1,53 | 1,00 | 1,91 | |
| Радиус кластера, Å | 3,78 | 3,75 | 3,72 | 3,81 | 4,38 | 3,90 | 6,65 |
Расположение встроенных электрических моментов отдельных атомов определяется минимумом потенциальной энергии обусловленной диполь-дипольным взаимодействием. На основании этого установлено расположение электрических моментов в различных кристаллических структурах кластерных образований. Для объемоцентрированной структуры расположение электрических моментов внутри кластера показано на рис. 88, а на рис. 89 приведено расположение встроенных дипольных электрических моментов ГЦК и гексагональной структуры кластера. Результирующий встроенный электрический момент с учетом взаимной компенсации для кластера ОЦК структуры составляет – 5 дипольных электрических моментов отдельного атома. Соответственно для ГЦК структуры – 3 и для гексагональной – 1. Структура алмаза представляет собой два встроенных друг в друга ГЦК структур, смещенных в направлении пространственной диагонали. Поэтому результирующий электрический момент кластера типа алмаза составит 6 дипольных электрических моментов отдельных атомов. На рис. 88 и рис. 89 центральный атом в кластере выделен, а размер кластера окаймлен пунктирным кругом.
При известном размере кластера, его энергии ионизации и величины дипольного электрического момента, можно произвести расчет энергии межкластерного взаимодействия, которое формирует решеточную структуру твердого тела.

Межкластерное взаимодействие. Ковалентная и ионная связь в межкластерном взаимодействии определяется по (8.34) и (8.35). При этом использовались данные по размерам и потенциалам ионизации, приведенные в табл. 8.1. Результаты расчета этих типов взаимодействия приведены в табл. 8.2. Так как размер кластера в три раза больше атомного размера, то ковалентная и ионная связь составляют небольшую величину по сравнению с межатомным взаимодействием внутри кластера.
Диполь-дипольное взаимодействие между кластерами соизмеримо с диполь-дипольным взаимодействием между атомами внутри кластера и даже равны друг другу. Вклад электрон-дипольного взаимодействия также составляет заметную величину. Получается, что результирующая энергия связи обратно пропорциональна расстоянию между кластерами в степени больше двух. Это приводит к хрупкому разрушению материалов, атомы которых обладают заметным встроенным электрическим моментом. Для марганца в основном реализуется хрупкое разрушение, кластер которого обладает мощным встроенным электрическим моментом (22,5 D).
Результаты расчета энергий связи электрон-дипольного и диполь-дипольного взаимодействия для кластеров различных веществ приведены в табл. 8.2. Диполь-дипольное взаимодействие выстраивает взаимодействующие системы во вполне определенном положении в пространстве. Дипольному электрическому моменту соответствует свой магнитный момент. Валентные электроны атомов внутри кластера и самих кластеров создают орбитальный магнитный момент, который расположен перпендикулярно электрическому моменту. В результате магнитные моменты также выстраиваются во вполне определенном направлении, образуя домены внутри кластера и между кластерами. Структура доменов соответствует рис. 88 и рис. 89. Ниже рассмотрим образование магнитных моментов в атомарных структурах и в кластерах. На основе этого выясним, как формируются доменные структуры.
Магнитные свойства атомов с достраивающимися d- и f- оболочками. Электрическому дипольному моменту соответствует магнитный дипольный момент, определяемый по формуле (8.33). Результаты расчета магнитных моментов различных атомов приведены в табл. 8.1.
 Диполь-дипольное взаимодействие внутри кластера выстраивает дипольные электрические моменты вдоль направления, которое обеспечивает минимум энергии взаимодействия. Магнитные моменты также выстраиваются вдоль одного направления перпендикулярно электрическому моменту. Взаимодействие магнитных моментов значительно уступает взаимодействию электрических моментов. Поэтому взаимодействием магнитных моментов в результирующей энергии связи можно пренебречь. Взаимодействие магнитных моментов с наложенным внешним магнитным полем может быть соизмеримо с диполь-дипольным взаимодействием электрических моментов. Этот тип магнитного взаимодействия следует учитывать в результирующей энергии связи.
Диполь-дипольное взаимодействие внутри кластера выстраивает дипольные электрические моменты вдоль направления, которое обеспечивает минимум энергии взаимодействия. Магнитные моменты также выстраиваются вдоль одного направления перпендикулярно электрическому моменту. Взаимодействие магнитных моментов значительно уступает взаимодействию электрических моментов. Поэтому взаимодействием магнитных моментов в результирующей энергии связи можно пренебречь. Взаимодействие магнитных моментов с наложенным внешним магнитным полем может быть соизмеримо с диполь-дипольным взаимодействием электрических моментов. Этот тип магнитного взаимодействия следует учитывать в результирующей энергии связи.
При наложении внешнего магнитного поля магнитные диполи вещества выстраиваются вдоль направления приложенного магнитного поля. Возникает ориентационная поляризация магнетика. Для связанных магнитных диполей взаимодействие магнитного диполя с внешним магнитным полем схематически приведено на рис. 90. Энергия взаимодействия магнитного диполя с внешним полем равна произведению
 . (8.38)
. (8.38)
Здесь рm – величина магнитного дипольного момента, а В – магнитная индукция внешнего магнитного поля
Количество диполей, которые повернутся вдоль приложенного внешнего поля на телесный угол dφ в сфероидальном конусе, преодолев энергию теплового движения, в соответствии с законом Больцмана составит:

При рm В соsφ/kbT << 1 можно закон Больцмана представить в виде ряда, ограничившись первым приближением, т.е.


Проинтегрировав (8.39) по всем телесным углам от нуля до π, получим: С` = n0/4π, где n0 –число частиц в единице объема, обладающих магнитным дипольным моментом.
Вектор магнитной поляризации по определению находится путем интегрирования следующего выражения:
 . (8.40)
. (8.40)
С учетом того, что  (κm – магнитная восприимчивость) и магнитное поле внутри магнетика
(κm – магнитная восприимчивость) и магнитное поле внутри магнетика  для магнитной восприимчивости и относительной магнитной проницаемости получаем:
для магнитной восприимчивости и относительной магнитной проницаемости получаем:
 . (8.41)
. (8.41)
Величина Wс введенная в (8.36а), определяет вероятность того, что магнитный диполь является связанным. Магнитная восприимчивость определяется количеством связанных магнитных диполей, а магнитная проницаемость в слабом магнитном поле определяется количеством свободных магнитных диполей в веществе при заданной температуре.
 В качестве примера рассмотрим поведение магнитной восприимчивости и магнитной проницаемости для железа. Результаты представлены на рис. 91 и рис. 92 соответственно. Аналогичные зависимости получаются и для других ферромагнитных материалов. Диполь-дипольное взаимодействие между кластерами выстраивает нанокластерные системы в определенном направлении, т.е. определяет магнитное упорядочивание в конденсированном состоянии. Температура, при которой происходит разрыв межкластерного диполь-дипольного взаимодействия элетрических диполей, называется температурой Нееля. Температура, при которой происходит разрыв взаимодействия электрических диполей отдельных атомных структур внутри кластера, называется температурой Кюри. Эффект резкого возрастания магнитной проницаемости ферромагнетиков в слабом магнитном поле вблизи температуры Кюри был открыт в 1889 г. Дж. Гопкинсоном и назван его именем (эффект Гопкинсона).
В качестве примера рассмотрим поведение магнитной восприимчивости и магнитной проницаемости для железа. Результаты представлены на рис. 91 и рис. 92 соответственно. Аналогичные зависимости получаются и для других ферромагнитных материалов. Диполь-дипольное взаимодействие между кластерами выстраивает нанокластерные системы в определенном направлении, т.е. определяет магнитное упорядочивание в конденсированном состоянии. Температура, при которой происходит разрыв межкластерного диполь-дипольного взаимодействия элетрических диполей, называется температурой Нееля. Температура, при которой происходит разрыв взаимодействия электрических диполей отдельных атомных структур внутри кластера, называется температурой Кюри. Эффект резкого возрастания магнитной проницаемости ферромагнетиков в слабом магнитном поле вблизи температуры Кюри был открыт в 1889 г. Дж. Гопкинсоном и назван его именем (эффект Гопкинсона).
Вычисленные значения температур Нееля и Кюри в пределах допущенных ошибок в расчетах полностью совпали с экспериментальными данными. Для атомных систем с гибридизацией d - и s -состояний энергия диполь-дипольного взаимодействия электрических диполей внутри кластера и между кластерами практически равны между собой. Поэтому для таких веществ в конденсированном состоянии температура Кюри совпадает с температурой Нееля. Для ряда атомных систем с гибридизацией f- и s- состояний энергия диполь-дипольного взаимодействия электрических диполей для атомов внутри кластера меньше, чем между кластерами. В этом случае температура Кюри меньше температуры Нееля.
Разработанная теория магнетизма позволила установить предельные значения намагничения ферромагнитных материалов. Так для железа это значение составило 230 А·м2/кг, что достаточно убедительно совпадает с экспериментальными данными.
Таким образом, ферромагнетизм обусловлен не образованием доменов вследствие спин-спинового взаимодействия, а возникает вследствие гибридизации волновых функций d(f)- и s -состояний. Это приводит к возникновению встроенных электрических моментов на уровне атомарных систем. Вследствие диполь-дипольного взаимодействия электрических диполей отдельных атомовпроисходит выстраивание магнитных моментов самопроизвольно внутри кластеров, а межкластерное взаимодействие приводит к образованию доменных структур в значительных объемах, когда температура не превосходит температуру Кюри. При температуре выше температуры Нееля диполь-дипольное взаимодействие не выстраивает магнитные моменты кластерных образований в заданном направлении, и вещество становится диамагнитным. Структурное строение определяет различную зависимость кривых намагничения от направления внешнего магнитного поля относительно кристаллографических осей. Коорцетивная сила обусловлена величиной энергии связи: ковалентной, ионной и электрон-дипольным взаимодействием.
Ферромагнитные домены. Область ферромагнитного тела, в которой магнитные моменты выстроены параллельно, называется доменом. Намагниченность в пределах каждого домена весьма велика. Если бы твердое тело состояло из одного домена, то даже в отсутствие приложенного магнитного поля оно должно было бы иметь большой результирующий магнитный момент, который создавал бы значительное внешнее магнитное поле, и тело обладало бы значительной магнитной энергией. Однако такого явления практически не наблюдается. Это обусловлено тем, что внутри ферромагнитного материала много таких доменов, которые в результате хаотического распределения компенсируют свои внешние поля. Требуется некоторая энергия на создание стенок между доменами. Реальная конфигурация доменов в каком-либо теле определяется минимумом суммы энергии магнитного поля, энергии стенок доменов и энергии анизотропии.
Величина и форма доменов поддается экспериментальной проверке. Наиболее прямой метод заключается в получении так называемых порошковых фигур. Если на хорошо отполированную поверхность ферромагнетика поместить слой жидкости со взвешенными мельчайшими крупинками ферромагнитного порошка, то крупинки будут оседать на те места, вблизи которых магнитное поле неоднородно, и этим самым очертят границы доменов.
Поиск по сайту: