 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
ЭМИССИОННЫЕ СВОЙСТВА КОНДЕНСИРОВАННЫХ СРЕД
Идеальную поверхность раздела «конденсированная среда-вакуум» можно представить как связанный между собой двойной электрический слой. Слой электронов и поверхностный слой положительно заряженных однократно ионизованных частиц внутрикластерной решеточной структуры. Каждый электрон поверхностного двойного слоя связан кулоновскими силами со своим однократно ионизованным атомом и находится в потенциальной яме. Величина потенциальной ямы определяется потенциалом двухчастичного взаимодействия.
Исходя из таких представлений под влиянием различных внешних воздействий (тепловое, электрическое, электромагнитное и др.) происходит эмиссия различных частиц с поверхности конденсированной среды. Внешнее воздействие в первую очередь воспринимают частицы двойного электрического слоя, а именно: однократно положительно заряженные ионы внутрикластерной решеточной структуры и электроны внешнего отрицательно заряженного облака. Поэтому с поверхности конденсированной среды в первую очередь в окружающую среду будут эмитировать однократно ионизованные ионы и электроны. Другие частицы в виде нейтральных атомов и отрицательно заряженных ионов должны покидать поверхность с меньшей вероятностью.
Наименьшая энергия, которую необходимо сообщить той или иной частице, чтобы она покинула поверхность материала, называется работой выхода. Работа выхода является основной фундаментальной константой, которая характеризует эмиссионные свойства того или иного материала. Рассмотрим теорию и практику получения этой константы с позиций кластерного строения конденсированной среды.
12.1. Работа выхода электронов, ионов и атомов
с поверхности конденсированной среды
Каждая частица, которая покидает поверхность, обладает своей работой выхода. Это обусловлено тем, что энергия связи внутри конденсированной среды для каждой частицы разная. Кроме этого по мере удаления от поверхности возникают силы взаимодействия между вылетающей частицей и поверхностью конденсированной среды, которые также отличаются от вещества к веществу. При этом важно знать, какими взаимодействиями формируется работа выхода для каждой из частиц в отдельности для различных веществ.
12.1.1. Работа выхода электронов с поверхности
конденсированной среды
В конденсированной среде электрон находится в потенциальной яме, глубина которой отсчитывается от границы ионизации до положения уровня Ферми*. Энергия потенциальной ямы с учетом смещения границы ионизации для некоторых веществ приведена в табл. 12.1.
Таблица 12.1.
Глубина потенциальной ямы ЕF для ряда элементов и работа выхода в нормальных условиях для различных плоскостей в эВ
| Пара- метры | Вещества | ||||||||
| Li | Na | Be | Al | Cu | α-Fe | Sr | Ba | W | |
| ЕF | 0,730 | 0,714 | 3,514 | 1,112 | 1,633 | 1,46 | 1,47 | 1,64 | 4,64 |
| {100} АВ , {110} {111} Поликристалл | 2,844 (2,61) 4,306 (4,24) 3,124 (3,25) 3,425 (3,45) | 2,454 (2,75) 3,716 (5,93) 2,696 (2,65) 3,208 (2,93) | 4,209 - 4,000 - 4,432 - 4,213 (3,92) | 2,421 (4,41) 2,300 (4,41) 2,561 (4,26) 2,428 (4,25) | 6,431 (5,61) 6,111 (4,92) 6,812 (5,54) 6,451 (5,5) | 4,057 (4,51) 6,143 - 4,456 (4,81) 4,886 (4,85) | 3,170 (2,43) 3,012 - 3,358 - 3,180 (2,74) | 3,190 (2,48) 4,830 – 3,504 – 3,841 (2,70) | 6,470 (6,25) 9,796 (7,2) 7,107 (5,3) 7,791 (6,76) |
Потенциальная яма, в которой находится электрон, для разных веществ заметно отличается друг от друга. Ранее считали, что работа выхода электрона определяется работой по преодолению двойного электрического слоя и по преодолению сил зеркального взаимодействия. При этом полагали, что работа по преодолению двойного электрического слоя составляет ~ 1 эВ. Однако механизм образования двойного электрического слоя вследствие выхода свободных электронов с поверхности конденсированного вещества не реализуется. На самом деле речь идет о преодолении электроном глубины потенциальной ямы, в которой он находится на уровне Ферми. Эту величину энергии необходимо учитывать в силах зеркального взаимодействия. Кроме этого не учитывалось, что электрон, который покидает поверхность, является свободным.
Внутри конденсированной среды электроны не свободные и это совершенно другие электроны. Они не могут покинуть поверхность, так как обладают спином и жестко связаны со своим силовым центром. Свободные электроны спином не обладают. Но только свободные электроны способны своим электрическим полем поляризовать поверхностный слой атомов в кластерных образованиях. Связанные электроны не могут выйти за пределы поверхности и оторваться от своих силовых центров. Тем не менее, они покидают поверхность. Следовательно, они в какой-то момент обладают свойствами свободного электрона. Действительно, в процессе обмена валентными электронами происходит переход от одной частицы к другой и при этом спин электрона изменяет свой момент на противоположное значение. В этот момент валентный электрон проходит через состояние свободного электрона. Вероятность такого перехода определяется величиной интеграла перекрытия.
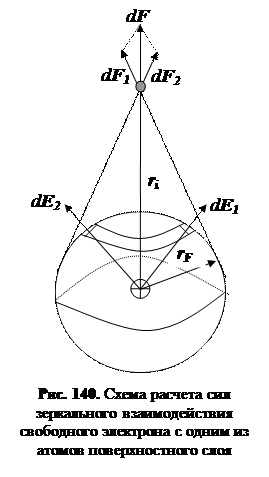 По мере удаления от поверхности свободный электрон поляризует каждый атом поверхностного слоя. Поэтому на небольших удалениях от поверхности происходит зеркальное взаимодействие не со всей поверхностью, а с отдельными атомами кристаллической решетки. Только на достаточно большом удалении от поверхности возникают силы «зеркального взаимодействия» в общепринятом понимании такой связи1.
По мере удаления от поверхности свободный электрон поляризует каждый атом поверхностного слоя. Поэтому на небольших удалениях от поверхности происходит зеркальное взаимодействие не со всей поверхностью, а с отдельными атомами кристаллической решетки. Только на достаточно большом удалении от поверхности возникают силы «зеркального взаимодействия» в общепринятом понимании такой связи1.
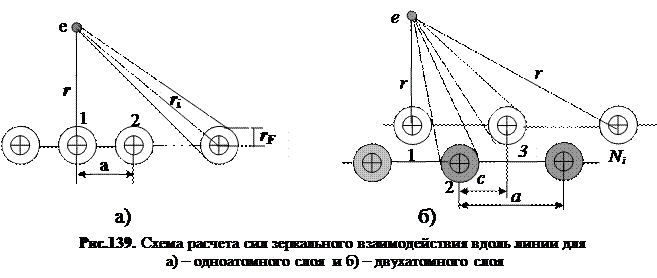
Схематично зеркальное взаимодействие свободного электрона с поверхностью конденсированной среды в одном из направлений показано на рис. 139, когда видны атомы только первого моноатомного слоя и когда видны атомы первого и второго моноатомных слоев. Основной вклад в работу выхода электрона с поверхности жидкого или твердого вещества составляют силы «зеркального взаимодействия».2) Речь идет о том, что электрон своим полем вызывает поляризацию атомов поверхностного слоя конденсированного состояния. С образовавшимся дипольным электрическим моментом электрон взаимодействует в соответствии с законом Кулона и принципом суперпозиции электрических полей. На рис. 140 показана схема расчета силы зеркального взаимодействия свободного электрона с одним из атомов поверхностного слоя.
Сила зеркального взаимодействия суммировалась по лучам. В качестве демонстрации как производятся вычисления, показана 1/8 часть поверхности {100} ОЦК структуры на рис. 141. Полученная сила проектировалась на нормаль к верхно-

сти и затем умножалась на восемь. Аналогично выполняется расчет для плоскости {110} ОЦК структуры. Для плоскости {111} ОЦК структуры выбиралась 1/12 часть поверхности, по которой производилось суммирование по отдельным атомам первого и второго моноатомных слоев. Полученное значение силы проектировалось на нормаль к поверхности и умножалось на 12. Результирующая сила умножалась на вероятность перехода связанного электрона через свободное состояние, и производилось интегрирование по нормали от радиуса поверхности Ферми rF до 10·rF. На удалении свыше 10· rF сила зеркального взаимодействия определялась по формуле
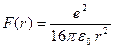 . (12.1)
. (12.1)
Из рис.140 следует, что сила зеркального взаимодействия свободного электрона с одним атомом первого или второго слоя с учетом затенения представится в виде:
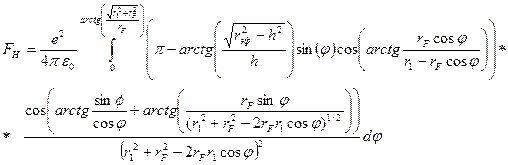 (12.2)
(12.2)
где 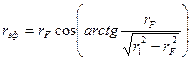 ;
; 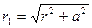 ;
; 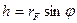 .
.
В результате окончательная формула для определения работы выхода электрона с металлической поверхности запишется так:
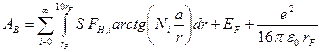 . (12.3)
. (12.3)
Здесь суммирование производится по каждому из лучей, а Ni - номер атома в луче. Интеграл перекрытия S усреднялся по всем состояниям валентного электрона внутри кластера.
Результаты расчета работы выхода по (12.3) для различных металлов приведены в табл.12.1. В скобках представлены значения, которые были получены различными авторами. Экспериментальные данные подчеркнуты. Совпадение расчетных значений с экспериментальными данными, полученных фотоэлектронным и термоэлектронным методом, вполне удовлетворительное. Что касается сравнения с теоретическими расчетами других авторов, то такое сравнение в ряде случаях приведено с целью демонстрации того, как это не следует делать, так как расчет любым из используемых моделей не соответствует реальной картине по самой постановке задачи.
По описанной выше методике был произведен расчет работы выхода для поверхности {100} стронция в зависимости от температуры без учета температурного расширения. Оказалось, что работа выхода в этом случае не изменяется с температурой. Отсюда следует, что работа выхода зависит от температуры преимущественно вследствие теплового расширения твердых тел. Как известно, это достаточно слабая зависимость. Для подтверждения этого вывода, в качестве примера, приведем расчет работы выхода от температуры для грани {100} меди. Полученный результат температурного коэффициента dAB/dT = 1,4·10-4 эВ/К отличается от экспериментально измеренного dAB/dT = 2,4·10-4 эВ/К незначительно.
Для поликристаллических веществ работа выхода в достаточно хорошем приближении может быть записана в виде:
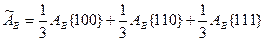 . (12.4)
. (12.4)
Результаты таких оценок также приведены в табл.12.1 в сравнении с экспериментальными данными, полученных термоэлектронным или фотоэлектронным методом.
 |
В случае диэлектриков электрическое поле, создаваемое свободным электроном, не достаточное, чтобы произвести заметную поляризацию атомов поверхностного слоя. Поэтому энергия взаимодействия «точечный заряд-диполь» является незначительной и таким взаимодействием можно пренебречь. Работа выхода в этом случае определяется только глубиной потенциальной ямы, в которой находится электрон. Это по существу энергия ионизации кластеров данного вещества. Работа выхода электрона для ковалентных кристаллов не зависит от состояния поверхности данного вещества.
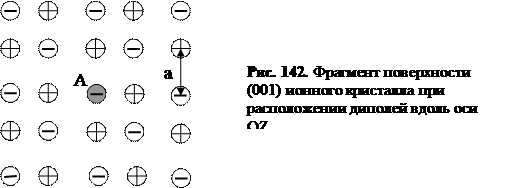
Для ионных кристаллов работа выхода электрона зависит от состояния поверхности. В качестве примера, рассмотрим, как формируется работа выхода электрона для ионных кристаллов NaCl, BaO, SrO, CaO, AlO, Al2O3, как это показано на рис. 142. Электрон с атома А покидает поверхность, которая сформирована знакопеременными электрическими зарядами. Для такой поверхности сила зеркального взаимодействия представится в виде:
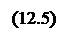
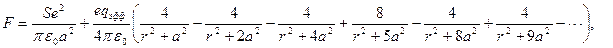 где qэфф – эффективный заряд электрического диполя.
где qэфф – эффективный заряд электрического диполя.
Работа выхода запишется так:
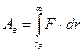 . (12.6)
. (12.6)
Здесь радиус rF – определяется как расстояние валентного электрона от центра молекулы. Конкретный расчет c указанием условий для ряда ионных кристаллов приведен в табл. 12.2.
Ионные кристаллы – это в основном нитриды, оксиды, хлориды и др., которые обладают большим встроенным электрическим моментом и являются хорошими диэлектриками. Работа выхода для таких веществ должна быть значительной. Выполненные конкретные измерения дают большой разброс по полученным результатам. Экспериментальные измерения термоэлектронным и фотоэлектронным методами3) выполнены в различных условиях их применения. Если проанализировать условия, в которых выполнялись измерения указанными методами, то их можно систематизировать в следующем порядке:
1) вещество содержит примеси;
2) измерения проведены в сильных электрических полях;
3) проведена активация в потоке другого вещества, обладающего металлическими свойствами;
4) тонкие пленки нанесены на металлический керн;
5) тонкие пленки экспонированы в среде кислорода или азота.
Каждый из указанных способов измерений вносит свои коррективы в полученный результат. Следует иметь в виду следующее обстоятельство. В ионном кристалле валентные электроны связаны с остовом кристаллической решетки, а в остове конкретно со своей молекулой. Энергия ионизации дипольных молекул составляет 5-10 эВ. Это значительная энергия связи. Чтобы валентные электроны перевести в разряд свободных необходимо затратить сравнительно большую работу. Если при этом учесть, что необходимо затратить еще работу по преодолению сил связи со знакопеременной поверхностью, то работа выхода с поверхностей ионных кристаллов должна быть значительной. Реально получают довольно низкие значения работ выхода с поверхностей ионных кристаллов. Это обусловлено тем, что свободные электроны поставляются в тело ионного кристалла независимым источником. В частности наличие примесей, которые взаимодействуют с дипольными молекулами адгезионными силами, приводит их к самопроизвольной ионизации и они в тело ионного кристалла поставляют свободные электроны. На это работа не тратится.
Наличие внешних электрических полей вызывают автоионизацию валентных электронов на отрицательном полюсе электрического диполя. Поэтому измерения работы выхода осуществляются в этом случае уже для свободных электронов.
Когда производят активацию, то на границах раздела возникают двойные электрические слои, которые являются как-бы положительно заряженной сеткой, и вследствие этого в тело ионного кристалла поставляют свободные электроны без затраты внешней работы.
Аналогичная ситуация возникает на границе раздела между керном и основным ионным кристаллом, а также при самопроизвольном росте оксидных слоев на основном материале, который является хорошим проводником и выполняет роль керна.
Таким образом, во всех рассмотренных случаях в теле ионного кристалла присутствуют свободные электроны, полученные независимым способом. При этом энергия на получение этих свободных электронов не учитывается при выполнении измерений. В процессе выполнения измерений учитывается только та часть работы, которая обусловлена взаимодействием уже свободного электрона со знакопеременной электрически заряженной поверхностью. Свободный электрон выходит на знакопеременную поверхность вблизи положительно заряженной части дипольного электрического момента. Ближайшее окружение составляют отрицательные заряды, которые заметно ослабляют взаимодействие выходящего электрона со знакопеременной поверхностью. В результате такого характера взаимодействия, как для связанных, так и для свободных электронов получается разброс значений работ выхода не только в измерениях, но и при выполнении теоретических расчетов.
Теоретический расчет работы выхода для ионных кристаллов был выполнен в следующих предположениях:
1 – работа затрачивается на то, чтобы с окончания отрицательно заряженного электрического диполя из связанного сформировать свободный электрон и затем учесть его взаимодействие со знакопеременной поверхностью;
2 – свободный электрон формируется внутри или за пределами остова ионного кристалла и выходит с конца отрицательного заряда электрического диполя;
3 – свободный электрон формируется внутри или за пределами остова ионного кристалла и выходит с положительного заряда электрического диполя.
Результаты выполненных расчетов приведены в табл.12.2.
Таблица 12.2.
Исходные данные для расчета работы выхода электрона и значение работы выхода для ряда ионных кристаллов.
| Параметры | Вещество | |||||
| NaCl | BaO | SrO | CaO | AlO | γAl2O3 | |
| Эффективный заряд | 0,708 | 0,733 | 0,729 | 0,707 | 0,759 | 0,759 |
| Энергия ионизации, эВ | 8,92 | 6,7 | 6,1 | 6,5 | 9,5 | 9,513 |
| Параметр решетки, Å | 5,639 | 5,542 | 5,083 | 4,812 | 4,833 | 7,895 |
| Работа выхода, эВ Свободный электрон | 3,49/4,2 4,2-2,39 1,24/- | 4,95/2,7 4,34-2,43 1,38/1,32 | 4,63/2,58 4,62-2,56 1,59/1,58 | 4,77/2,53 4,74-2,62 1,61/1,60 | 7,09/- 5,2-2,9 1,57/- | 6,21/5,08 3,25-1,55 0,91/3,20 |
Наиболее вероятная ситуация для свободного электрона реализуется та, которая сформулирована в третьем предположении. Для этого случая получено хорошее совпадение с опытными данными, когда вещество нанесено на металлический керн, который поставляет свободные электроны в тело ионного кристалла. Эта ситуация используется при создании термоэлектронных катодов. Как наилучшим способом реализовать термоэлектронный катод, рассмотрим ниже.
12.1.2. Работа выхода ионов и атомов с поверхности
конденсированных сред
При достаточно высоких температурах с поверхности твердого тела или жидкости будут испаряться свободные частицы из межкластерных пустот и связанные частицы основного кластера данного вещества. Как для свободных, так и для связанных частиц работа выхода будет определяться энергией связи частиц в основном кластере при заданной температуре. На основании кластерного строения конденсированных сред свободные частицы взаимодействуют с кластерами, которые следует рассматривать как некие макромолекулы. Энергия ионизации таких молекул для ряда веществ приведена в табл. 12. 1. Получается, что взаимодействие осуществляется между разными частицами одного и того же вещества. При взаимодействии разных частиц возникает определенная доля ионной связи. Так как кластеры – это большие молекулы, поэтому при взаимодействии свободных частиц с кластером последние могут пребывать с определенной вероятностью в виде нейтральных атомов, положительных или отрицательных ионов. Например, для вольфрама свободные атомы при взаимодействии с кластером обладают вероятностью пребывания в виде положительного иона Р1 = 0,298, а в виде отрицательного иона – Р2 = 0,206. Вероятность пребывания в виде нейтрального атома составляет: Р3 = 1- (Р1 + Р2) ~ 0,496. Поэтому эмиссия атомов вольфрама с его поверхности может происходить в виде нейтральных атомов, положительных или отрицательных ионов. Для связанных атомов в самом кластере валентные электроны обобщены, а ионы формируют внутрикластерную решеточную структуру (ионный остов), т.е. реализуется модель строения типа «макроатома» по Томсону, но с упорядоченной структурой.
Так для атомов вольфрама при температуре 2750 К энергия связи частиц основного кластера имеет значение 8,69 эВ. Экспериментальное значение теплоты испарения вольфрама при указанной температуре составляет 8,6 ± 0,4 эВ. Получается, что при указанной температуре энергия связи частиц основного кластера вольфрама соответствует теплоте испарения нейтральных атомов вольфрама.
В процессе испарения положительных ионов следует дополнительно учитывать силы зеркального взаимодействия. Для вольфрама работа по преодолению сил зеркального взаимодействия равна 1,655 эВ. Результирующая энергия связи для иона вольфрама равна 10,4 эВ, а экспериментальное значение - 11,8 ± 0,4 эВ. Для отрицательных ионов работа выхода должна быть такой же величины, как для положительно заряженных ионов.
Для измерения работы выхода используют метод контактной разности потенциалов. При этом предполагают, что контактная разность потенциалов определяется преимущественно разностью работ выхода. Однако это не так. Рассмотрим явление контактной разности потенциалов с позиций кластерного строения твердых тел.
Поиск по сайту: