Колебания электромагнитного поля в RLC-контуре

Принципиальная электрическая схема RLC -контура приведена на рис. 114. От источника ЭДС ключом К заряжается электроемкость С до напряжения источника тока U_э и затем отключается. Энергия, которая при этом была передана RLC -контуру, равна . (10.18)

После отключения источника ЭДС ключом К возникает замкнутая система в неравновесных условиях с пассивной окружающей средой. Стремление такой системы к равновесию приведет к тому, что электроемкость С начнет разряжаться через сопротивление R и индуктивность L. В цепи возникнут две стоячие волны: электрическая и магнитная. Вследствие этого энергия электрического поля, запасенная в электроемкости, будет переходить в энергию магнитного поля, сосредоточенной в индуктивности L и частично расходоваться на ленцаджоулевое тепло. Закон сохранения энергии в этом случае в момент времени t запишется в виде:

. (10.19)

Возьмем производную от правой и левой частей полученного равенства по времени t. Производная от интеграла с переменным верхним пределом равна подынтегральной функции. Учитывая это, будем иметь:

. (10.20)

Так как 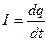, а , то после сокращения на 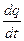получим:

. (10.21)

Левая часть равенства (10.21) представляет собой падение напряжения на электроемкости, падение напряжения на резисторе и ЭДС самоиндукции. Равенство (10.21) представим в более компактной форме

. (10.22)

После деления на L равенство (10.22) будет иметь вид:

. (10.23)

Уравнение (10.23) по виду не отличается от уравнения обычных механических затухающих колебаний

,

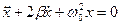в котором β – коэффициент затухания и ω₀ – частота собственных колебаний колеблющейся системы, а решением является:

. (10.24)

Сравнивая (10.23) и (10.24), получаем:

и . (10.25)

Логарифмический декремент затухания определяется через отношение амплитуд колебаний за период и имеет вид:

. (10.26)

Вместо логарифмического декремента затухания часто применяют пропорциональную ему величину , называемую затуханием.

Для характеристики колебательных контуров употребляют величину, называемую добротностью. Добротность Q есть величина, обратная затуханию d: . (10.27)

Добротность характеризует резонансные свойства системы, поэтому к понятию добротности возвратимся при рассмотрении вынужденных колебаний.

В нелинейных системах отношение потерь энергии за период к полной энергии колебаний не остается постоянным, а меняется с изменением амплитуды колебаний. Поэтому последующие амплитуды не подчиняются закону затухающих колебаний, т.е. не образуют геометрическую прогрессию. Простейшая нелинейная система – это когда внутри конденсатора содержится сегнетоэлектрик, а внутри индуктивности – ферромагнетик.

Поиск по сайту: