 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Явление термоэлектронной эмиссии
В 1883 г. Эдисон обнаружил, что многие вещества при сравнительно низких температурах испускают электроны. Это явление получило название термоэлектронная эмиссия. Основываясь на классической электронной теории металлов, Ричардсон получил формулу для плотности тока насыщения:
 . (12.11)
. (12.11)
Исходя из термодинамических соображений и квантовой теории, Дэшмен получил несколько другую формулу
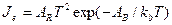 . (12.12)
. (12.12)
Первые серьезные экспериментальные исследования выявили несоответствие предложенных формул для описания термоэлектронной эмиссии. При наложении сравнительно слабых электрических полей наблюдались волнообразные колебания тока эмиссии около прямой Шоттки ( , где UB – межэлектродный потенциал). Пришлось предположить, что электроны, проходя потенциальный барьер, должны отражаться от стенок этого барьера, и в результате интерференции электронных волн, возникает периодическое изменение тока эмиссии. Вследствие этого в формулу (12.12) пришлось ввести интерференционный член, а именно:
, где UB – межэлектродный потенциал). Пришлось предположить, что электроны, проходя потенциальный барьер, должны отражаться от стенок этого барьера, и в результате интерференции электронных волн, возникает периодическое изменение тока эмиссии. Вследствие этого в формулу (12.12) пришлось ввести интерференционный член, а именно:
 . (12.13)
. (12.13)
Здесь D – коэффициент отражения электронов на границе металл-вакуум.
Выражение (12.13) известно как уравнение Ричардсона-Лауэ-Дэшмена. Известный специалист по эмиссионным свойствам веществ Модинос А. сложившуюся ситуацию комментирует следующим образом: «Следует отметить, что отражение электрона от границы металл-вакуум и обусловленные им явления не поддаются точному анализу даже в приближении свободных электронов, так как в большинстве случаев отражение электронов у границы тесно связано с кристаллической природой металла и зонной структурой его энергетических уровней».
Видоизменяя форму потенциального барьера можно легко согласовать формулу (12.13) с данными эксперимента. Но это уже чистая эмпирика. Если не изменять вид потенциального барьера как это следует из определения такого барьера, то волнообразное поведение тока эмиссии должно возникать с постоянной амплитудой. Экспериментально наблюдаются разные амплитуды. Кроме этого формулы, описывающие термоэлектронную эмиссию, получены на основании модели «свободных электронов», которых в твердых телах просто нет. Природа термоэлектронной эмиссии несколько иная.
 Атомы в кластерных образованиях пребывают в виде положительных ионов. Колебания этих ионов относительно положения равновесия обуславливает выход электронов с поверхности конденсированных сред. Конкретно эту ситуацию рассмотрим на примере вольфрама. Для описания колебаний атомов в кластерных структурах следует использовать не квантовую статистику, а максвелл-больцмановскую статистику. При нормальных температурах частицы третьей координационной сферы обычно свободные и находятся в межкластерных пустотах, обеспечивая обменное межкластерное взаимодействие. Совершают колебания преимущественно частицы второй координационной сферы. Потенциал взаимодействия частиц второй координационной сферы для кластерных образований вольфрама для разных температур приведен на рис. 143. До температуры плавления вольфрам пребывает в виде кристаллического состояния, а выше температуры плавления – в виде жидкого состояния. Атомы второй координационной сферы в кластерном образовании пребывают в виде положительных ионов, которые с повышением температуры совершают колебательное движение с амплитудой, как показано на рис 144 стрелками. На рис. 144 также показан фрагмент колебания положительного иона на поверхности кристалла.
Атомы в кластерных образованиях пребывают в виде положительных ионов. Колебания этих ионов относительно положения равновесия обуславливает выход электронов с поверхности конденсированных сред. Конкретно эту ситуацию рассмотрим на примере вольфрама. Для описания колебаний атомов в кластерных структурах следует использовать не квантовую статистику, а максвелл-больцмановскую статистику. При нормальных температурах частицы третьей координационной сферы обычно свободные и находятся в межкластерных пустотах, обеспечивая обменное межкластерное взаимодействие. Совершают колебания преимущественно частицы второй координационной сферы. Потенциал взаимодействия частиц второй координационной сферы для кластерных образований вольфрама для разных температур приведен на рис. 143. До температуры плавления вольфрам пребывает в виде кристаллического состояния, а выше температуры плавления – в виде жидкого состояния. Атомы второй координационной сферы в кластерном образовании пребывают в виде положительных ионов, которые с повышением температуры совершают колебательное движение с амплитудой, как показано на рис 144 стрелками. На рис. 144 также показан фрагмент колебания положительного иона на поверхности кристалла.
При движении иона вглубь кристалла расстояние между электроном, находящимся на ферми поверхности уменьшается на величину Δr и взаимодействие между положительным ионом и электроном возрастает, а с электроном, находящегося на внешней поверхности, наоборот уменьшается. Разность этих энергий расходуется на возбуждение валентных электронов кластера. Если эта энергия больше работы выхода электрона, то произойдет выброс электрона в окружающую среду, т.е. возникнет термоэлектронная эмиссия. Это произойдет в том случае, когда ион сместится относительно положения равновесия на величину

 . (12.14)
. (12.14)
Например, для вольфрама эта величина составляет всего 0,3 Å, а rF имеет значение 1,37 Å. Плотность тока термоэлектронной эмиссии определится по формуле:  . (12.15)
. (12.15)
где γ – доля эмитируемых электронов с одного кластера, mа – масса кластера при температуре Т, Rкл. – радиус кластера.
Число центров эмиссии определяется чистотой обработки поверхности, т.е. величиной шероховатости. Кроме этого следует также учитывать и «многочастичную» эмиссию, которая наблюдалась экспериментально. Как шероховатость, так и многочастичная эмиссия существенным образом сказываются на величине доли эмитируемых электронов с одного кластера.
Плотность тока термоэлектронной эмиссии в зависимости от температуры для различных плоскостей монокристалла вольфрама приведена в табл. 12.5.
Таблица 12.5.
Плотность тока термоэмиссии (А/м2) в зависимости от температуры для различных идеальных поверхностей вольфрама при одноэлектронном механизме
| Поверх- ность | Температура, К | |||||
| {100} | 3,97·10-18 | 5,73·10-2 | 1,29·104 | 4,29·105 | 5,89·106 | |
| {110} | 1,03·10-34 | 3,57·10-10 | 2,78·10-5 | 4,98·10-2 | 10,4 | |
| {111} | 2,69·10-21 | 1,56·10-3 | 5,35 | 1,20·103 | 5,68·104 | 1,02·106 |
Выполненный теоретический расчет для различных плоскостей вольфрама свидетельствует о том, что только при достаточно высоких температурах возникает заметная термоэмиссия электронов из вольфрама. Это подтверждается экспериментальными данными.
Конкретные измерения термоэлектронной эмиссии с поверхности поликристаллического вольфрама дали значения при температуре 2500 К – 1000 А/м2, а при температуре 2700 К – 4000 А/м2. Решая обратную задачу в соответствии с (12.15), получаем значение работы выхода 5,93 – 6,09 эВ. Если учесть шероховатость, то полученная работа выхода должна иметь меньшее значение по сравнению с идеальной поверхностью.
 При проведении исследований термоэмиссионных свойств материалов необходимо измерять термоэмиссионный электрический ток. Для этого используют метод задерживающего потенциала или метод совместного применения термо- и автоэлектронной эмиссии, как это в свое время предложил Шоттки. Идея Шоттки сводилась к тому, что наложение внешнего слабого электрического поля заметно не должно уменьшать работу выхода и поэтому измерение эмиссионного тока должно соответствовать термоэмиссионному току. При этом предполагалось, что поверхность идеальная и не имеет шероховатостей. При наличии шероховатостей на отдельных выступах внешнее поле может возрастать в сотни раз, а на отдельных кластерах в 109 раз. Для полированной поверхности вольфрама это возрастание составило ~ 100 - 300 раз. Когда происходит несколько пробоев импульсами электрического разряда, коэффициент усиления падает до 20 – 25 раз, а при прогреве при температурах 1000 – 27000 С этот коэффициент уменьшался до 10 – 20 раз. Учитывая это обстоятельство, при слабом внешнем электрическом поле на микровыступах могли реализоваться электрические поля, соответствующие заметной автоэлектронной эмиссии. Рассмотрим теорию Шоттки с учетом высказанных замечаний.
При проведении исследований термоэмиссионных свойств материалов необходимо измерять термоэмиссионный электрический ток. Для этого используют метод задерживающего потенциала или метод совместного применения термо- и автоэлектронной эмиссии, как это в свое время предложил Шоттки. Идея Шоттки сводилась к тому, что наложение внешнего слабого электрического поля заметно не должно уменьшать работу выхода и поэтому измерение эмиссионного тока должно соответствовать термоэмиссионному току. При этом предполагалось, что поверхность идеальная и не имеет шероховатостей. При наличии шероховатостей на отдельных выступах внешнее поле может возрастать в сотни раз, а на отдельных кластерах в 109 раз. Для полированной поверхности вольфрама это возрастание составило ~ 100 - 300 раз. Когда происходит несколько пробоев импульсами электрического разряда, коэффициент усиления падает до 20 – 25 раз, а при прогреве при температурах 1000 – 27000 С этот коэффициент уменьшался до 10 – 20 раз. Учитывая это обстоятельство, при слабом внешнем электрическом поле на микровыступах могли реализоваться электрические поля, соответствующие заметной автоэлектронной эмиссии. Рассмотрим теорию Шоттки с учетом высказанных замечаний.
Зная величину силы зеркального взаимодействия ( ), построим распределение потенциала, соответствующий этой силе (рис. 145). Кривая 1 является гиперболой и асимптотически приближается к оси ОZ. Распределение потенциала внешнего поля представляется кривой 2 (
), построим распределение потенциала, соответствующий этой силе (рис. 145). Кривая 1 является гиперболой и асимптотически приближается к оси ОZ. Распределение потенциала внешнего поля представляется кривой 2 ( ). Результирующий потенциал является суммой этих двух кривых и изображен на рис. 145 кривой 3. Кривая 3 имеет минимум, который определяет область, с которой электроны ускоряются под действием внешнего электрического поля. Это значит, что работа выхода уменьшается на величину потенциала, соответствующего точке минимума результирующего потенциала. Найдя первую производную по z и приравняв ее нулю, находим то значение, на которое уменьшилась работа выхода, а именно:
). Результирующий потенциал является суммой этих двух кривых и изображен на рис. 145 кривой 3. Кривая 3 имеет минимум, который определяет область, с которой электроны ускоряются под действием внешнего электрического поля. Это значит, что работа выхода уменьшается на величину потенциала, соответствующего точке минимума результирующего потенциала. Найдя первую производную по z и приравняв ее нулю, находим то значение, на которое уменьшилась работа выхода, а именно:
 . (12.16)
. (12.16)
В результате формула (12.15) с учетом (12.16) запишется так:
 . (12.17)
. (12.17)
В полученной формуле не учтено следующее обстоятельство. Наличие больших электрических полей на выступах микронеровностей приводит к возникновению пондеромоторных сил, которые деформируют выступ, и как бы сглаживают его. Разогрев микровыступов существенно ослабляет модуль Юнга, и под влиянием сил поверхностного натяжения микровыступы сглаживаются в большей мере. Возрастание радиуса микровыступа приводит к увеличению работы выхода за счет уменьшения  и за счет включения новых центров, на которых наводятся заряды противоположного знака. Одновременно новые центры являются дополнительными источниками электронной эмиссии. Получается весьма сложная зависимость термоэмиссионного тока от приложенного внешнего электрического поля.
и за счет включения новых центров, на которых наводятся заряды противоположного знака. Одновременно новые центры являются дополнительными источниками электронной эмиссии. Получается весьма сложная зависимость термоэмиссионного тока от приложенного внешнего электрического поля.
Пондеромоторные силы создают давление на поверхность микровыступа
 . (12.18)
. (12.18)
Под действием такого давления произойдет деформация на величину  (где Е – модуль Юнга). Например, для микровыступа с головкой радиуса 0,125 мм с учетом того, что эффективный размер плоского участка составляет 0,01 стерадиан, получаем радиус плоского эмиссионного пятна 1,25·10-6 м. Тогда количество эмиссионных центров (кластеров) на радиусе такого пятна на вольфраме составит 3000. Если под действием пондеромоторных сил радиус возрастет на один кластерный монослой, то
(где Е – модуль Юнга). Например, для микровыступа с головкой радиуса 0,125 мм с учетом того, что эффективный размер плоского участка составляет 0,01 стерадиан, получаем радиус плоского эмиссионного пятна 1,25·10-6 м. Тогда количество эмиссионных центров (кластеров) на радиусе такого пятна на вольфраме составит 3000. Если под действием пондеромоторных сил радиус возрастет на один кластерный монослой, то  = 0,1%. Это упругая область деформации. Такая деформация возникнет под давлением 1,5·106 Па, которое обеспечивает напряженность электрического поля 5,8·108 В/м. С увеличением напряженности внешнего электрического поля скачками будет возрастать радиус плоской части выступа на два, три и т.д. кластерных монослоев. В этом случае попеременно будет то возрастать, то уменьшаться эффективная величина работы выхода. Поэтому и наблюдается периодическое отклонение эмиссионного тока от линии Шоттки. При термоэмиссии с поверхностей ионных кристаллов ситуация периодического отклонения от линии Шоттки должна быть более выражена. Это обусловлено тем, что по мере увеличения кластерной плоской поверхности слой за слоем работа выхода то возрастает, то уменьшается. На примере зависимости работы выхода от количества атомов на радиусе плоской поверхности
= 0,1%. Это упругая область деформации. Такая деформация возникнет под давлением 1,5·106 Па, которое обеспечивает напряженность электрического поля 5,8·108 В/м. С увеличением напряженности внешнего электрического поля скачками будет возрастать радиус плоской части выступа на два, три и т.д. кластерных монослоев. В этом случае попеременно будет то возрастать, то уменьшаться эффективная величина работы выхода. Поэтому и наблюдается периодическое отклонение эмиссионного тока от линии Шоттки. При термоэмиссии с поверхностей ионных кристаллов ситуация периодического отклонения от линии Шоттки должна быть более выражена. Это обусловлено тем, что по мере увеличения кластерной плоской поверхности слой за слоем работа выхода то возрастает, то уменьшается. На примере зависимости работы выхода от количества атомов на радиусе плоской поверхности
 |
кластеров Al2O3 это хорошо видно на рис. 146.
Аналогичная ситуация имеет место для всех поверхностей ионных кристаллов. Для поликристаллических поверхностей периодические отклонения от прямой Шоттки будут несколько сглажены, но присутствие такого отклонения должно иметь место.
Поиск по сайту: