АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Магнитное напряжение. Закон полного тока

Читайте также:
  1. B) Наличное бытие закона
  2. II закон Кирхгофа
  3. II. Законодательные акты Украины
  4. II. Законодательство об охране труда
  5. II.3. Закон как категория публичного права
  6. III. Государственный надзор и контроль за соблюдением законодательства об охране труда
  7. IX. У припущенні про розподіл ознаки по закону Пуассона обчислити теоретичні частоти, перевірити погодженість теоретичних і фактичних частот на основі критерію Ястремського.
  8. IX.3.Закономерности развития науки.
  9. А 55. ЗАКОНОМІРНОСТІ ДІЇ КОЛОГИЧЕСКИХ ФАКТОРІВ НА ЖИВІ ОРГАНІЗМИ
  10. А) Закон диалектического синтеза
  11. А) полного профиля б) неполного профиля в) отсутствие прорези
  12. А) совокупность предусмотренных законодательством видов и ставок налога, принципов, форм и методов их установления.

По аналогии с электрическим напряжением , которое для замкнутого контура равно нулю , введем напряжение магнитного поля. Магнитное напряжение на участке dl (рис. 96) равно , (8.42)

где - проекция элемента некоторого контура на направление .

Пусть магнитное поле создается прямолинейным проводником. Тогда

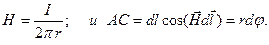
Следовательно,

. (8.43)

Магнитное напряжение на участке dl не зависит от расстоя­ния этого участка до токонесущего провода. Если взять интеграл по замкнутому контуру, то

. (8.44)

Величина называется циркуляцией вектора напряженности магнитного поля или магнитодвижущей силой. Магнитодвижущая сила по любому замкнутому контуру, охватывающему ток, равна этому току.

Если замкнутый контур охватывает несколько токов, то

;

.

Учитывая это, окончательно получим:

. (8.45)

Выражение (8.45) определяет закон полного тока, который формулируется следующим образом: циркуляция вектора напряженности магнитного поля вдоль любого замкнутого контура, охватывающего несколько электрических токов, равна алгебраической сумме токов с учетом их знаков.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 121 | 122 | 123 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)