Примеры решения задач. До конца осознать и понять физическую сущность уравнений Максвелла - общих уравнений электромагнитного поля

До конца осознать и понять физическую сущность уравнений Максвелла - общих уравнений электромагнитного поля, содержащих в себе все основные законы электромагнетизма, можно путем решения конкретных практических задач. Рассмотрим некоторые из них.

Пример 1. Соленоид имеет длину l = 0,2 м; площадь поперечного сечения S = 10^-3 м² и число витков N = 400. Соленоид находится в диамагнитной среде, индуктивность его L =10^-3 Гн. Найти магнитную индукцию и вектор намагничения внутри соленоида, если по соленоиду проходит ток величиной I = 2 A.

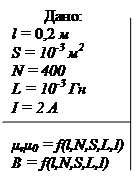Р е ш е н и е

1. Магнитная индукция В связана с напряженностью Н соотношением 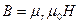. При этом H = w₀I, а магнитную проницаемость можно выразить формулой 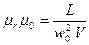, объем соленоида V = lS = 0,2∙10^-3 м³. Подставляя в формулу для магнитной индукции выражения напряженности и магнитной проницаемости, получим:

.

В системе СИ:

О т в е т: В = 5 мТл.

2. Вектор намагничения 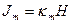, где — магнитная восприимчивость среды. Но 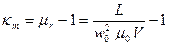, а .

Тогда .

В системе СИ: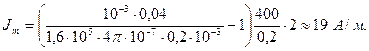

О т в е т: Вектор намагничения J_m однозначно определяет индукцию поля 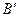, созданного микротоками среды.

Пример 2. Электрон в возбужденном атоме водорода находится в 3 р -состоянии. Определить изменение магнитного момента, обусловленного орбитальным движением электрона, при переходе атома в основное состояние.

Р е ш е н и е.

Изменение магнитного момента найдем как разность магнитных моментов: , где и - магнитный момент возбужденного и основного состояния соответственно.

Магнитный момент орбитального движения зависит от азимутального квантового числа l следующим образом

,

где - магнетон Бора. В основном состоянии и в возбужденном состоянии и .

Изменение магнитного момента равно:

Подставив значение μ_Б =0,927.10^-23 Дж/Тл, получим: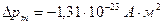

О т в е т: Знак «-» показывает, что в данном случае магнитный момент уменьшается.

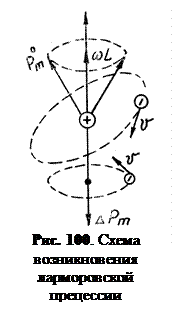Пример 3. Определить частоту ларморовой прецессии электронной орбиты в атоме, если индукция магнитного поля В = 1 Тл.

Р е ш е н и е

Согласно теореме Лармора, результатом влияния магнитного ноля на электронную орбиту является прецессия орбиты и вектора магнитного момента p_m вокруг оси, проходящей через центр орбиты и параллельной магнитному полю Н, причем частота прецессии , где - гиромагнитное отношение орбитального движения. Тогда

.

Подставим значения в системе СИ:

О т в е т: Угловая скорость прецессии направлена вдоль поля В. За счет прецессии орбиты возникает дополнительный ток i_пр, который создает магнитный момент (рис. 100), направленный против внешнего намагничивающего поля. Этот момент является диамагнитным моментом атома.

Пример 4. По медному проводу, сечением которого является круг, имеющий радиус 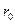= 2 см, течет ток I = 500 А. Определить индукцию в точках, отстоящих от оси провода на расстоянии 0,5 и 5 см. Построить график зависимости B=f(r).

Р е ш е н и е

Из закона полного тока (8.42) в соответствии с рис. 101 следует, что

,

где I₁ ток, сцепленный с контуром L₁ и равный

.

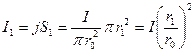Во всех точках контура L₁ величина магнитной индукции постоянная. Относительная магнитная проницаемость для меди практически равна единице. Поэтому

.

Так как 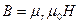, то .

Следовательно, внутри медного провода магнитная индукция возрастает по линейному закону. Вне проводника при r₂ > r₀ имеем

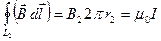
или .

Вне проводника магнитная индукция падает обратно пропорционально расстоянию от оси проводника. Общее распределение магнитной индукции вдоль радиуса приведено на рис. 101.

Произведем вычисления в системе СИ:

О т в е т: .

Пример 5. Электрон вращается по окружности, радиус которой равен 10 см, в переменном магнитном поле (рис. 102). Индукция магнитного поля изменяется от 3 до 11 Тл за время 10^-3 с. Определить изменение энергии электрона и частоту излучения электромагнитных волн, если он успевает сделать 10⁴ оборотов.

Р е ш е н и е

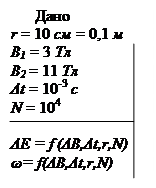С переменным магнитным полем в соответствии с уравнениями Максвелла связано электрическое поле, силовые линии которого замкнуты и имеют вид окружностей, охватывающих переменный магнитный поток. Электрон, попав в такое поле, будет вращаться по одной из силовых линий.

Изменение энергии электрона определится работой, которую совершает вихревое электрическое поле при перемещении электрона по окружности, имеющей радиус r, т.е.

где

Здесь знак «минус» указывает, что направление вектора _э связано с направлением вектора 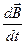правилом левого винта. Опустив знак «минус», запишем

В системе СИ имеем:

Электрон, вращаясь по окружности, радиус которой r, излучает на циклотронной частоте, равной: Тогда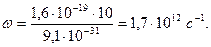

О т в е т. Энергия электрона увеличится на 314 кэВ, а частота циклотронного излучения будет равна 1,7∙10¹² с^-1.

Пример 6. Какое изменение магнитного поля необходимо обеспечить, чтобы стабилизировать плазменный шнур диаметром 5 мм путем создания круговых токов на поверхности шнура со скоростью вращения электронов 5∙10⁷ м/с за время 0,1 с? Сколько при этом оборотов совершит электрон?

Р е ш е н и е

Из решения предыдущей задачи следует, что под влиянием изменяющегося магнитного поля в толще плазменного шнура кинетическая энергия вращения электронов возрастает от оси к периферии как квадрат радиуса. Следовательно, скорость пропорциональна радиусу. Поэтому максимальная скорость вращения электронов реализуется на поверхности плазменного шнура. Чтобы придать электрону дополнительную энергию, необходимо поместить его в электрическое поле Е_э. На электрон будет действовать сила, и он начнет двигаться с ускорением 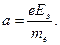Поскольку начальная скорость равна нулю, то .

Напряженность вихревого электрического поля определяется в соответствии с законом электромагнитной индукции Фарадея следующим образом:

.

Отсюда по абсолютной величине

.

Окончательно с учетом полученного выражения для напряженности электрического поля скорость вращения электрона равна

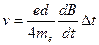или .

В системе СИ имеем:

Количество оборотов, которое совершит электрон, найдем так:

.

Вычисления дают:

О т в е т: Изменение магнитной индукции в единицу времени равно 2,28 Тл/с, а общее число оборотов, которые совершит электрон, составит 1,6∙10⁸.

Поиск по сайту: