Электрон в магнитном поле

Возвращаясь к силе Лоренца, из которой вытекает равенство (5.22), умножим это равенство на заряд электрона. Тогда или в векторной форме . В общем случае на любой заряд q движущийся в магнитном поле в отсутствие электрического поля будет действовать сила Лоренца

. (6.19)

Направление действия силы Лоренца определяется векторным произведением (6.19) или правилом левой руки, так же как и направление действия силы магнитного поля на проводник с током (рис. 57). При этом вытянутые пальцы следует направить вдоль движения положительного заряда (если это отрицательный заряд, то против него).

Рассмотрим некоторые особенности силы Лоренца. Когда частица с массой т и зарядом q влетает в однородное магнитное поле перпендикулярно направлению вектора магнитной индукции В со скоростью v, то сила Лоренца будет равна

(6.20)

и перпендикулярна к вектору скорости v. Это значит, что она имеет характер центростремительной силы. Следовательно, эти силы можно приравнять и найти радиус окружности движения заряженной частицы в магнитном поле: . (6.21)

Время, за которое совершается один оборот по этой окружности, равно

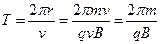. (6.22)

Период вращения не зависит от скорости заряженной частицы и от радиуса. Этот факт используется в приборах, служащих для разгона заряженных частиц (циклотроне, бетатроне).

Если же заряженная частица движется с ускорением, то она излучает. Излучение, обусловленное действием силы Лоренца, носит название циклотронного излучения. Частота излучения в соответствии с (6.22) определяется так:

. (6.23)

Циклотронное излучение возникает, если плазму поместить в магнитное поле. Этот вид излучения играет существенную роль в термоядерном синтезе, где потери на циклотронное излучение могут быть соизмеримы с энергией выхода при ядерной реакции, что является препятствием, которое необходимо преодолеть при реализации термоядерного синтеза.

Движущийся электрон в магнитном поле излучает на циклотронной частоте, и это используется в магнетронах для генерирования СВЧ колебаний.

Рассмотрим случай, когда заряженная частица влетает в магнитное поле под углом. Вектор скорости тогда можно разложить на две составляющие: параллельно и перпендикулярно полю. Параллельная составляющая не изменяется в магнитном поле, а перпендикулярная изменяется по направлению под действием силы Лоренца. Частица как бы навинчивается на магнитную силовую линию (рис. 58).

В этой связи при наложении магнитного поля на плазму заряженные частицы плазмы нанизываются на магнитную силовую линию, т.е. будут завязаны в магнитном поле. Такие электроны уже не свободны и не взаимодействуют с падающей электромагнитной волной. Плазма в этом случае просветляется для прохождения электромагнитных волн, и через нее могут проходить элект­ромагнитные сигналы. Рассмотренный эффект используется для осуществления непрерывной связи с космическими кораблями и баллистическими ракетами, когда они совершают полет в плотных слоях атмосферы, и вокруг них возникает достаточно плотная плазма, препятствующая прохождению электромагнитных волн.

Если движущийся электрический заряд находится одновременно как в магнитном, так и в электрическом поле, то результирующая сила

. (6.24)

Это одно из основных уравнений магнитной гидродинамики, которое было получено ранее – формула (5.21).

В качестве примера рассмотрим движение электрического заряда во взаимно перпендикулярных электрических и магнитных полях, как изображено на рис. 59. При этом силы действуют на заряд в противоположные стороны. На заряженную частицу, движущуюся вдоль пластин конденсатора (ось Z) перпендикулярно линиям электрического поля, действует сила Под действием этой силы заряженная частица (электрон) вдоль оси Y будет двигаться равноускоренно. Смещение по оси Y равно

(6.25)

Здесь время 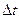может быть выражено через скорость частицы по оси Z так: Тогда

(6.26)

Отсюда видно, что электрон, влетая перпендикулярно электрическому полю, движется по параболе. Если регистрирующий экран отстоит от плоского конденсатора на удалении l_{2 ,} то общее смещение электронного пучка равно сумме (6.27)

где

Чтобы компенсировать общее смещение электронного пучка за счет воздействия электрического поля, нужно перпендикулярно линиям электрического поля наложить магнитное поле. Магнитное поле можно подобрать такой величины, чтобы оно своим действием компенсировало силы воздействия со стороны электрического поля. В этом случае

(6.28) или (6.29)

Но так как то легко получить удельный заряд электрона:

(6.30)

Такой метод определения удельного заряда электрона был предложен Дж. Томсоном. В системе СИ удельный заряд электрона равен 1,76∙10¹¹ Кл/кг.

Опыт Дж. Томсона по существу является обоснованием взаимодействия движущегося электрического заряда с электромагнитной волной.

Поиск по сайту: