Вынужденные колебания. Чтобы колебания частицы в вязкой среде были гармоническими (с постоянной амплитудой ), к частице надо приложить вынужденную силу:

Чтобы колебания частицы в вязкой среде были гармоническими (с постоянной амплитудой ), к частице надо приложить вынужденную силу:

(12.1)

где положительные постоянные 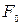и ω — амплитуда и круговая частота колебаний силы соответственно.

С учетом вынуждающей силы дифференциальное уравнение (11.3) принимает вид

(12.2)

Решение уравнения (12.2) дает закон движения частицы, называемый вынужденными колебаниями частицы,

(12.3)

где

(12.4)

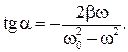(12.5)

Из выражения (12.4) видно, что амплитуда колебаний частицы зависит от круговой частоты ω колебаний вынуждающей силы . Найдем частоту при которой амплитуда имеет максимальное значение. Очевидно, что при 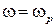подкоренное выражение в соотношении (12.4) должно быть минимальным, т. е. при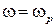

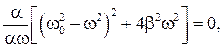
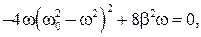
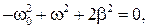
откуда

(12.6)

Круговую частоту называют резонансной частотой. Резкое возрастание амплитуды выраженных колебаний частицы при частоте ω колебаний вынуждающей силы равной резонансной, называют явлением резонанса.

Поиск по сайту: