АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Закон Джоуля – Ленца. При перемещении заряда dq по проводнику силы электрического поля совершают работу

Читайте также:
  1. B) Наличное бытие закона
  2. II закон Кирхгофа
  3. II. Законодательные акты Украины
  4. II. Законодательство об охране труда
  5. II.3. Закон как категория публичного права
  6. III. Государственный надзор и контроль за соблюдением законодательства об охране труда
  7. IX. У припущенні про розподіл ознаки по закону Пуассона обчислити теоретичні частоти, перевірити погодженість теоретичних і фактичних частот на основі критерію Ястремського.
  8. IX.3.Закономерности развития науки.
  9. А 55. ЗАКОНОМІРНОСТІ ДІЇ КОЛОГИЧЕСКИХ ФАКТОРІВ НА ЖИВІ ОРГАНІЗМИ
  10. А) Закон диалектического синтеза
  11. А) совокупность предусмотренных законодательством видов и ставок налога, принципов, форм и методов их установления.
  12. А. Законодательные (представительные) органы власти республик в составе Российской Федерации

 

 

При перемещении заряда dq по проводнику силы электрического поля совершают работу

 

(46.1)

 

где — напряжение на концах проводника. Подставив dq из выражения (43.1) в соотношение (46.1), получаем

 

(46.2)

 

Величину

 

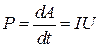(46.3)

 

назовем мощностью тока, развиваемой в проводнике. С учетом закона Ома (44.1) мощность тока можно записать в виде

 

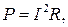(46.4)

 

где R — сопротивление проводника.

Если проводник неподвижен и в нем не происходят химические превращения, работа (46.2) идет на увеличение внутренней энергии проводника, в результате чего проводник нагревается. Можем написать

 

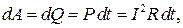(46.5)

 

откуда, интегрируя, получаем

 

(46.6)

 

где Q — количество теплоты, выделяемой в проводнике при протекании в нем электрического тока в течение времени (закон Джоуля – Ленца).

Соотношение (46.6) называют законом Джоуля – Ленца в интегральной форме. Найдем дифференциальную форму этого закона.

  Рис. 46.1 Для этого выделим мысленно в окрестности некоторой точки проводника элементарный объем в виде цилиндра высотой d ℓ и площадью основания dS с образующими, параллельными плотности тока 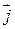в этой точке (рис. 46.1). Тогда, согласно выражениям (46.4) и (46.5), в этом объеме за время dt выделится количество теплоты

 

(46.7)

 

где — объем цилиндра.

Подставив в выражение (46.3) вместо работы dA количество теплоты dQ, получим тепловую мощность тока

 

(46.8)

 

— количество теплоты, выделяемое в проводнике в единицу времени. Назовем удельной тепловой мощностью тока величину

 

(46.9)

 

— количество теплоты, выделяемое в единицу времени в единице объема проводника.

С учетом выражение (46.7) и (46.9) можем написать

 

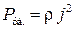(46.10)

 

— удельная тепловая мощность тока в некоторой точке проводника равна произведению удельного сопротивления проводника на квадрат плотности тока в этой точке (закон Джоуля – Ленца в дифференциальной форме).

Комбинируя законы Ома (44.6) и Джоуля – Ленца (46.10), получаем выражение для удельной тепловой мощности тока в виде

 

(46.11)

 

Пример 46.1. Сила тока в проводнике сопротивлением нарастает в течение по линейному закону от до . Определить количество теплоты Q, выделившееся в этом проводнике за вторую секунду.

Дано: Решение  
 
 
.


Согласно условию задачи,

 

 

где коэффициент k определяет скорость возрастания тока
q –?

 

 

 

 

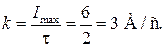
Согласно условию задачи,

 

 

Ответ: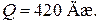


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.005 сек.)