 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Средняя скорость и среднее ускорение
Из математики известно, что среднее значение функции  (скалярной или векторной) на промежутке от
(скалярной или векторной) на промежутке от 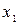 до
до  определяется выражением
определяется выражением
 (5.1)
(5.1)
Если известны зависимости скорости  и ускорения
и ускорения 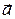 частицы от времени
частицы от времени 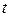 при ее движении по траектории, то, используя выражение (5.1), можно определить их средние значения за любой промежуток времени
при ее движении по траектории, то, используя выражение (5.1), можно определить их средние значения за любой промежуток времени 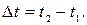 Можно написать
Можно написать
 (5.2)
(5.2)
 (5.3)
(5.3)
Аналогично можно записать выражения для средних значений модуля вектора и его проекций на координатные оси, например, на ось x:
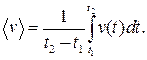 (5.4)
(5.4)
 (5.5)
(5.5)
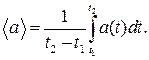 (5.6)
(5.6)
 (5.7)
(5.7)
В случае вращения твердого тела имеем
 (5.8)
(5.8)
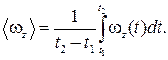 (5.9)
(5.9)
 (5.10)
(5.10)
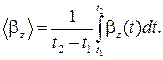 (5.11)
(5.11)
Пример 5.1. Закон движения частицы 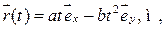

 Найти среднюю скорость
Найти среднюю скорость  частицы за промежуток времени от t 1=2 с до t 2=4 с.
частицы за промежуток времени от t 1=2 с до t 2=4 с.
Дано:
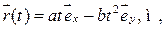

 t 1=2 с
t 2=4 с
t 1=2 с
t 2=4 с
| Решение

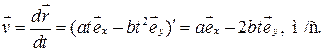
|
 –? –?
|
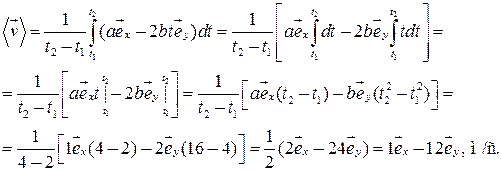
 Ответ:
Ответ: 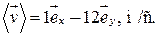
Пример 5.2. Закон вращения тела  где a = 6 рад/c, b = = 2 рад/с3. Найти средний модуль
где a = 6 рад/c, b = = 2 рад/с3. Найти средний модуль 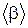 углового ускорения тела за промежуток времени от
углового ускорения тела за промежуток времени от  до момента
до момента  остановки тела.
остановки тела.
Дано:

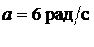


| Решение
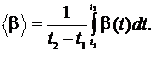


 
|
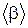 –? –? 
|

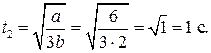
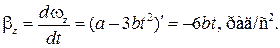
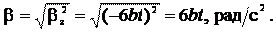

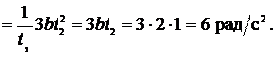
Ответ: 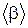 = 6 рад/с2.
= 6 рад/с2.
Поиск по сайту: