Плоская гармоническая волна

Пусть фронт плоской гармонической волны распространяется в направлении оси x. Обозначим через ξ смещение в момент времени 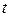любой частицы относительно ее положения равновесия, которое задается координатой оси .

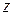В этом случае волновые поверхности будут представлять плоскости, перпендикулярные к оси . Все частицы, имеющие одну и ту же координату , но разные и , будут принадлежать одной и той же волновой поверхности — плоскости x = const и колебаться одинаковым образом, т. е. ξ будет зависеть только от и 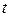. В связи с этим поставленную задачу можно свести к рассмотрению колебаний частиц, положения равновесия которых лежат на оси .

Если колебание частиц, лежащих в плоскости , имеют вид

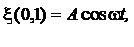
то в плоскости, соответствующей произвольному значению , колебания частиц будут отставать по времени на τ от колебаний частиц в плоскости . Отставание связано с тем, что волна пройдет путь от плоскости до плоскости за время где v — скорость распространения волны. Можем написать

(14.1)

Введем волновое число

(14.2)

где λ — длина волны. С учетом формул (10.6) и (13.2) перепишем выражение (14.2) в виде

(14.3)

С учетом соотношения (14.3) уравнение (14.1) примет вид

(14.4)

Уравнение (14.4) является уравнением плоской гармонической волны, распространяющейся в направлении оси . Уравнение волны, распространяющейся противоположно направлению оси , отличается от уравнения (14.4) только знаком плюс при .

Уравнение (14.4) является решением дифференциального уравнения. Получим его. Для этого дважды продифференцируем ξ по и :

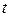(14.5)

откуда

(14.6)

Подставляя выражение (14.6) в соотношение (14.5), получаем

или, с учетом формулы (14.3), получаем окончательно

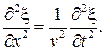(14.7)

Дифференциальное уравнение (14.7) называют волновым уравнением плоской гармонической волны, распространяющейся вдоль оси .

ЭКЗАМЕНАЦИОННЫЕ ВОПРОСЫ 1

1. Путь и перемещение.

2. Скорость.

3. Ускорение.

4. Сила и основное уравнение динамики.

5. Работа и мощность силы.

6. Угловая скорость и угловое ускорение.

7. Момент силы и основное уравнение динамики вращения твердого тела.

8. Механическая энергия и ее связь с работой.

9. Закон сохранения механической энергии.

10. Импульс. Закон сохранения импульса.

11. Момент импульса. Закон сохранения момента импульса.

12. Гармонические колебания.

13. Затухающие колебания.

14 Вынужденные колебания.

15. Гармонические волны.

16. Плоская гармоническая волна.

Поиск по сайту: