Распределение Максвелла

Назовем состояние газа равновесным,если параметры состояния газа при отсутствии внешних воздействий остаются неизменными во времени.

Пусть газ находится в равновесном состоянии при температуре . Молекулы газа, непрерывно сталкиваясь между собой, меняют свои скорости как по направлению, так и по величине. Мы не можем сказать, с какой скоростью станет двигаться произвольно выбранная молекула в тот или иной момент времени. В то же самое время мы можем говорить о некотором стационарном (устойчивом) распределении молекул по скоростям: одни молекулы движутся быстро, другие медленно. Но на всякий интервал скоростей, например от 10 до 20 м/с или от 20 до 30 м/с, будет приходиться в среднем (по времени) некоторое определенное число молекул. При отсутствии внешних воздействий установившееся при данной температуре распределение молекул по скоростям в дальнейшем не изменяется.

Определим вероятность того, что модуль скорости молекулы лежит между v и v + dv. Пусть 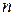— общее число молекул в единице объема газа, а — число молекул в единице объема газа, скорости которых лежат между v и v + dv. Тогда искомая вероятность

(17.1)

Введем величину

(17.2)

— плотность вероятности, которая является функцией модуля скорости молекулы, в связи с чем ее называют функцией распределения вероятности молекул по скорости или просто функцией распределения молекул по скоростям.

Комбинируя формулы (17.1) и (17.2), получаем

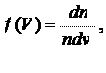(17.3)

откуда

(17.4)

Зная вид функции f (v), можно, интегрируя выражение (17.4), определить количество молекул в единице объема газа, скорости которых лежат в любом интервале скоростей.

Максвелл теоретически получил вид функции распределения молекул по скоростям:

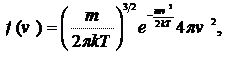(17.5)

где и — масса молекулы и температура газа; 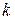— постоянная Больцмана.

Изобразим график функции (17.5) (рис. 17.1).

Рис. 17.1

Из графика видно, что вероятность обнаружения в газе молекулы со скоростью, лежащей в интервале от v ₁ до v ₂ (см. формулу (17.2))

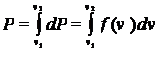
равна заштрихованной площади под кривой f (v).

Вероятность обнаружения в газе молекул с любой скоростью от 0 до

(17.6)

т. е. площадь под всей кривой f (v) равна единице. Выражение (17.6) называют условием нормировки вероятности.

Скорость, соответствующая максимуму функции распределения f (v), будет наиболее вероятной v _вер скоростью молекул. Найдем эту скорость.

Для очевидно

Продифференцируем выражение (17.5) по v и приравняем к нулю.

При v = 0 и v = ∞ функция f (v) минимальна. Следовательно, эти значения отбрасываем. Остается

откуда

Откуда получаем

(17.7)

Используя функцию распределения (17.5), можно найти среднюю и среднюю квадратичную v _кв скорости молекул:

(17.8)

(17.9)

Поиск по сайту: