Поляризация диэлектрика

Диэлектриками называют вещества, практически не проводящие электрического тока. В диэлектриках нет заряженных частиц, способных свободно перемещаться (в отличие от проводников) на значительные расстояния, создавая электрический ток.

Диэлектрики состоят либо из нейтральных молекул, либо из заряженных ионов, находящихся в узлах кристаллической решетки (NaCl). Молекулы могут быть полярными (H₂O, спирты, поливинилхлорид) и неполярными (H₂, N₂, O₂, CCl₄). У полярных молекул центр тяжести отрицательных зарядов сдвинут относительно центра тяжести положительных зарядов, в результате чего они обладают собственным электрическим (дипольным) моментом . Дипольные моменты полярных молекул ориентированы хаотически из-за теплового движения молекул. Неполярные молекулы собственным дипольным моментом не обладают. У них центры тяжести положительных и отрицательных зарядов совпадают.

Под действием внешнего электрического поля с напряженностью происходит поляризация диэлектрика. Дипольные моменты полярных молекул устанавливаются по полю . В пределах каждой неполярной молекулы происходит смещение зарядов — положительных по полю, отрицательных против поля, вследствие чего неполярные молекулы приобретают дипольные моменты, ориентированные по полю. В ионных кристаллах также все положительные ионы смещаются по полю, отрицательные — против поля.

Для количественного описания поляризации диэлектрика берут дипольный момент единицы объема диэлектрика:

(38.1)

где — сумма дипольных моментов N молекул, заключенных в элементарном (очень малом) объеме 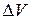диэлектрика. Вектор называют поляризованностью диэлектрика.

На рис. 38.1 изображен схематически поляризованный однородный диэлектрик. Из рисунка видно, что поляризация сопровождается возникновением в тонком поверхностном слое диэлектрика избытка зарядов одного знака. Так как свобода перемещения этих зарядов ограничена в пределах молекулы, их называют связанными, в отличие от зарядов, не входящих в состав молекул диэлектрика и поэтому называемых сторонними. Сторонние заряды могут находиться как внутри, так и вне диэлектрика.

Рис. 38.1

В результате появления нескомпенсированных связанных зарядов на поверхности диэлектрика в нем возникает электрическое поле связанных зарядов. Напряженность поля в диэлектрике равна сумме напряженностей поля сторонних зарядов (внешнего поля) и поля связанных зарядов:

(38.2)

§ 39. Вектор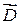

Теорема Гаусса для поля вектора в диэлектрике имеет вид

(39.1)

где q и 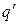— сторонние и связанные заряды, охватываемые замкнутой поверхностью S.

Расчет вектора в диэлектрике с использованием соотношения (39.1) затруднителен, так как заранее не известно распределение связанных зарядов в электрическом поле. Это затруднение можно обойти, воспользовавшись теоремой Гаусса для поля вектора :

(39.2)

поток вектора сквозь любую замкнутую поверхность S равен , где — избыточный связанный заряд внутри этой поверхности.

Подставляя

в соотношение (39.1), получаем

откуда

(39.3)

Введем вектор

(39.4)

и запишем выражение потока вектора 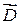в виде

(39.5)

которое представляет теорему Гаусса для поля вектора 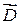: поток вектора 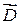сквозь любую замкнутую поверхность S равен 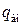, где 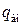— алгебраическая сумма сторонних зарядов внутри этой поверхности.

Поле вектора 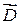можно изобразить наглядно с помощью линий вектора 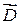, которые проводят аналогично линиям вектора (см. § 32). Однако, если лини вектора могут начинаться и заканчиваться как на сторонних, так и на связанных зарядах, то линии вектора 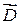могут начинаться и заканчиваться только на сторонних зарядах.

Для изотропных диэлектриков

(39.6)

где æ — безразмерная положительная величина, называемая диэлектрической восприимчивостью вещества. Эта величина не зависит от и является характеристикой диэлектрика.

Подставляя выражение (39.6) в соотношение (39.4), получаем

или

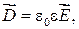(39.7)

где — безразмерная положительная величина, называемая диэлектрической проницаемостью вещества. Эта величина, как и æ, является характеристикой диэлектрика. Для вакуума , для воздуха , для всех других веществ .

Из соотношения (39.7) имеем

(39.8)

Следовательно, используя теорему Гаусса для поля вектора 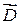, можно определить вектор 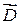в любой точке электрического поля в диэлектрике, а затем по формуле (39.8) найти напряженность поля в этой точке.

Пример 39.1. Имеем равномерно заряженную сферу с зарядом q, находящуюся в среде с диэлектрической проницаемостью ε. Радиус сферы R. Определить потенциал φ электрического поля на поверхности сферы.

Дано:   q   ε   R	Решение   Для нахождения потенциала φ воспользуемся соотношением (36.10). Получим зависимость напряженности E поля, создаваемого сферой, от расстояния r от центра сферы при . Возьмем любую точку вне сферы на расстоянии r от центра сферы. Вследствие симметрии вектор 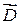поля, создаваемого сферой, в этой точке направлен радиально от центра сферы.
φ –?
Рис. 39.1	Определим модуль (длину) этого вектора. Проведем через интересующую нас точку гауссову замкнутую поверхность S в виде сферы радиусом r с центром в точке О (рис. 39.1). Найдем поток вектора 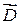сквозь гауссову поверхность: (39.9)

При интегрировании мы учли, что для всех точек гауссовой сферы α = 0 и D = const.

Согласно теореме Гаусса

(39.10)

(из рис. 39.1 видно, что заряженная сфера находится внутри гауссовой поверхности и поэтому заряд 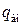равен заряду q сферы).

Подставляя выражение (39.9) в соотношение (39.10), получаем

откуда

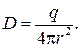(39.11)

Воспользовавшись соотношением (39.8), находим напряженность E:

(39.12)

Подставим выражение (39.12) в соотношение (36.10) и проинтегрируем:

(при интегрировании мы приняли и ). Следовательно, на поверхности сферы, а также во всех точках внутри сферы (см. выражение (36.11)) потенциал

(39.13)

Поиск по сайту: