 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Уравнение состояния идеального газа
Согласно кинетической теории, газ представляет собой большое число молекул, находящихся в непрерывном хаотическом тепловом движении. Свойства газов (например, давление и температура) являются суммарным результатом действия молекул.
Рассмотрим модель идеального газа. Согласно этой модели молекулы газа — это маленькие шарики, суммарный объем которых всегда пренебрежимо мал по сравнению с объемом сосуда, в котором они находятся. Шарики не взаимодействуют между собой на расстоянии, а только непрерывно упруго сталкиваются друг с другом, двигаясь до соудорения прямолинейно и равномерно.
Получим уравнение состояния идеального газа — уравнение, связывающее параметры состояния газа — давление P, объем  и температуру
и температуру  (в кельвинах).
(в кельвинах).
Опыт показывает, что при небольших давлениях легкие газы, такие как водород и гелий, с хорошей точностью подчиняются уравнению
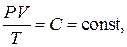 (15.1)
(15.1)
называемому уравнением Клапейрона. Следовательно, уравнение (15.1) можно считать уравнением состояния идеального газа. Постоянная 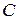 зависит от химического состава и количества газа.
зависит от химического состава и количества газа.
Обозначим через 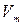 объема одного моля газа. Подставляя
объема одного моля газа. Подставляя  где
где  — число молей газа, в уравнение (15.1), имеем
— число молей газа, в уравнение (15.1), имеем

откуда

(15.2)
где постоянная  не зависит от количества газа. Кроме того, так как, согласно закону Авогадро, моли различных газов при одинаковых давлениях и температурах имеют одинаковый объем, постоянная
не зависит от количества газа. Кроме того, так как, согласно закону Авогадро, моли различных газов при одинаковых давлениях и температурах имеют одинаковый объем, постоянная

(15.3)
не зависит от химического состава газа, т. е. одинакова для всех газов. Поэтому ее принято называть универсальной газовой постоянной.
Найдем численное значение  . Известно, что при нормальных условиях
. Известно, что при нормальных условиях  1 атм =
1 атм = 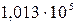 Па,
Па,  =273 К) объем моля газа
=273 К) объем моля газа 
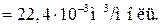 Согласно соотношению (15.3)
Согласно соотношению (15.3)

Подставляя  в уравнение (15.1), получаем уравнение состояния идеального газа
в уравнение (15.1), получаем уравнение состояния идеального газа

 (15.4)
(15.4)
называемое уравнением Клапейрона – Менделеева.
Пример 15.1. В баллоне вместимостью  находится аргон под давлением
находится аргон под давлением  и при температуре
и при температуре  Когда из баллона было взято некоторое количество газа, давление в баллоне понизилось до
Когда из баллона было взято некоторое количество газа, давление в баллоне понизилось до 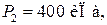 а температура установилась
а температура установилась  Определить массу
Определить массу 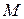 аргона, взятого из баллона.
аргона, взятого из баллона.
Дано:



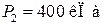

| Решение
 (Масса газа
(Масса газа 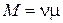 , где μ — масса моля
газа; , где μ — масса моля
газа;  — число молей газа). — число молей газа).
 . .
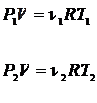

| ||||||
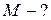
|
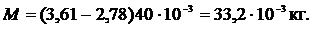
(см. Приложение Б).
Ответ: M = 33,2 г.
Пример 15.2. В баллонах объемом  и
и  содержится газ. Давление в первом баллоне
содержится газ. Давление в первом баллоне 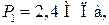 во втором —
во втором —  Определить давление
Определить давление 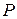 после соединение баллонов, если температура газа осталась прежней.
после соединение баллонов, если температура газа осталась прежней.
Дано:


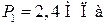

| Решение
 

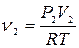
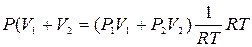
| ||||||||

|
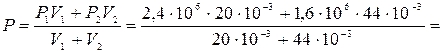
= 1,85·106 Па.
Ответ: P =1,85·МПа.
Поиск по сайту:
