Импульс. Закон сохранения импульса

Назовем импульсом частицы векторную величину , равную произведению массы частицы на ее скорость:

(8.1)

Из соотношения (8.1) видно, что направление импульса совпадает с направлением скорости.

С учетом основного уравнения динамики частицы

можем написать

(8.2)

производная по времени от импульса частицы равна действующей на нее силе.

Рассмотрим систему, состоящую из определенного числа частиц. Назовем внешними частицами все частицы, не входящие в рассматриваемую систему частиц. Соответственно назовем внешними силами силы, действующие на частицы системы со стороны внешних частиц, а внутренними силами — силы взаимодействия между частицами системы.

Опыт показывает (третий закон механики Ньютона), что каждая пара частиц системы взаимодействует с равными по модулю силами, направленными в противоположные стороны, откуда следует, что результирующая сила, действующая на эти частицы, равна нулю. Обобщая на всю систему частиц, можно сказать, что сумма всех внутренних сил в системе равна нулю. Следовательно, если в выражениях (8.2) — суммарный импульс всех частиц системы, то — результирующая внешних сил, действующих на систему.

Назовем систему частиц замкнутой, если на нее не действуют внешние силы или результирующая внешних сил равна нулю. Для такой системы имеем

или

(8.3)

импульс замкнутой системы частиц остается постоянным (закон сохранения импульса).

Пример 8.1. На полу стоит тележка в виде длинной доски, снабженной легкими колесами. На одном конце доски стоит человек. Масса человека масса тележки Найти, на какое расстояние передвинется тележка, если человек перейдет на другой конец доски. Длина доски Массой колес и трением пренебречь.

Дано:	Решение

где — модуль скорости тележки; 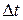— время движения человека по доске.

(по закону сохранения импульса),

(по закону сложения скоростей),

где и — скорости человека и тележки относительно пола; — скорость человека относительно тележки (рис. 8.1).

Рис. 8.1

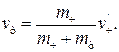
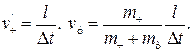
Ответ: S = 1,5 м.

Поиск по сайту: