Момент импульса. Закон сохранения момента импульса

Пусть частица с массой движется по траектории. В момент времени 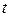ее импульс 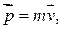а положение в пространстве определяет радиус-вектор , проведенный из точки 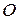, являющейся началом координат (рис. 9.1).

Назовем моментом импульса частицы относительно точки 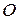вектор 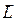, равный векторному произведению векторов и :

Рис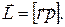. 9.1

(9.1)

Направления векторов 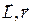и связаны правилом правого винта, если направить указательный палец правой руки по вектору , а средний — по вектору , то отогнутый большой палец покажет направление вектора 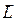(рис. 9.1). Модуль момента импульса

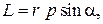(9.2)

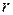где и 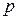— модули векторов и — угол между векторами и .

Назовем прямую, вдоль которой направлен импульс, линией действия импульса, а расстояние от линии действия импульса до точки 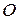— плечом импульса относительно точки 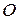. Как видно из рис. 9.1,

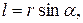
откуда

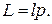
(9.3)

Проекции 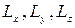вектора 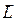на координатные оси называют моментами импульса частицы относительно этих осей. Например, — момент импульса частицы относительно оси .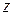

Продифференцируем выражение (9.1) по времени:

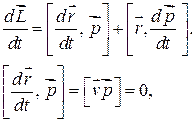
так как 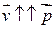(вектор совпадает по направлению с вектором ).

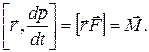
Таким образом,

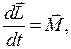
(9.4)

производная по времени от момента импульса частицы равна действующему на нее моменту силы.

Рассмотрим систему, состоящую из определенного числа частиц. Согласно третьему закону механики Ньютона, внутренние силы, действующие на каждую пару взаимодействующих частиц системы, одинаковы по модулю, противоположны по направлению и лежат на одной прямой, т. е. имеют одинаковое плечо. Поэтому моменты сил, действующих на каждую пару частиц системы, равны по модулю и противоположны по направлению, т. е. уравновешивают друг друга. Обобщая на всю систему частиц, можно сказать, что суммарный момент всех внутренних сил равен нулю. Следовательно, если в выражении (9.4) 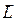— суммарный момент импульсов всех частиц системы, то — суммарный момент всех внешних сил.

Для замкнутой системы частиц имеем

или

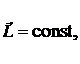(9.5)

момент импульса замкнутой системы частиц остается постоянным (закон сохранения момента импульса).

Закон сохранения момента импульса выполняется и для твердого тела, вращающегося вокруг неподвижной оси. Расчет дает, что момент импульса твердого тела относительно оси вращения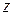

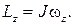(9.6)

Пример 9.1. Человек массой m _ч стоит на краю горизонтального диска массой m _д, который может свободно вращаться вокруг неподвижной вертикальной оси 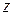, проходящей через его центр. В некоторый момент времени человек начал двигаться по краю диска и совершил перемещение на угол , после того остановился. Считая человека частицей, найти угол , на который повернулся диск при перемещении человека.

Дано: m ч   m д	Решение 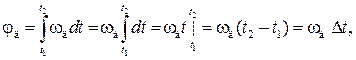где ωд — модуль угловой скорости диска; 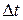  — время перемещения человека.
–?

В проекциях на ось вращения 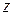можем написать

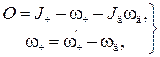
где 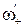— угловая скорость человека относительно диска.

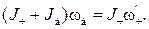
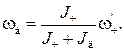
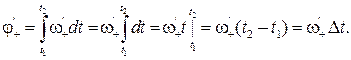
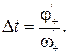
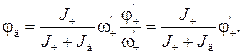
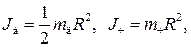
где — радиус диска.

Ответ: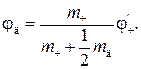

Поиск по сайту: