Вынужденные колебания при гармоническом внешнем воздействии. Резонанс колебаний

В том случае, когда на колебательную систему оказывается периодическое внешнее воздействие, подчиняющееся гармоническому закону, колебания описываются уравнением вида:

, (7.3.1)

где, также как и для случая затухающих свободных колебаний, - коэффициент затухания, - собственная частота системы, т.е. частота, с которой совершались бы колебания в отсутствии затухания, - частота вынуждающего воздействия на систему.

Выражение для коэффициента зависит от вида колебательной системы и внешнего воздействия. Например, для пружинного маятника , где - амплитуда вынуждающей силы (рис 7.3.1). Для вынужденных колебаний в колебательном контуре: , где - амплитуда переменного напряжения, подаваемого на колебательный контур, - индуктивность (рис 7.3.2).

Общее решение такого неоднородного дифференциального уравнения (7.3.1) равно сумме общего решения соответствующего однородного уравнения (7.1.1) и частного решения неоднородного уравнения. Эти два слагаемых соответствуют свободным затухающим колебаниям и незатухающим

колебаниям с частотой вынуждающей силы. По истечении некоторого промежутка времени решение уравнения (7.3.1) будет совпадать с частным решением.

Описываемый им режим движения называется установившимся режимом вынужденных колебаний. Соответству­ющее выражение имеет вид

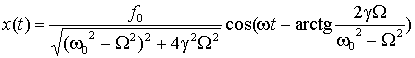. (7.3.2)

Амплитуда вынужденных колебаний зависит от частоты вынуждающей силы:

. (7.3.3)

Величина

(7.3.4)

характеризует отставание по фазе вынужденного колебания от обусловившего это колебание внешнего воздействия. Следует отметить, что установившиеся колебания происходят с частотой вынуждающего воздействия W, а не с собственной частотой. При W=0 выражение (7.3.3) дает статическое отклонение

. (7.3.5)

Зависимость амплитуды вынужденных колебаний от частоты вынуждающего воздействия (рис. 7.3.3) приводит к тому, что при некоторой определенной для данной колебательной системы частоте амплитуда колебаний достигает максимального значения. Резкое возрастание амплитуды вынужденных колебаний при приближении частоты внешнего воздействия к некоторому значению называют явлением резонанса (резонансом). Резонансную частоту находят, приравнивая нулю производную , откуда

, (7.3.6)

. (7.3.7)

Для механических колебаний при резонансной частоте внешнего воздействия, определяемой по формуле (7.3.6), достигается максимум амплитуды смещения колеблющейся величины , для электромагнитных колебаний в контуре - максимум амплитуды заряда q(t). Максимум амплитуды производной (соответственно, скорости или тока) достигается при . Максимум амплитуды второй производной (соответственно, ускорения или напряжения на катушке индуктивности) достигается при . Максимум средней мощности внешнего воздействия (для механических колебаний максимум мощности внешней силы ) достигается при . Если затухание невелико, то положения всех перечисленных максимумов почти не отличаются друг от друга. При малом затухании:

, . (7.3.8)

В данном случае, добротность Q показывает, во сколько раз амплитуда в момент резонанса a _рез превышает отклонение системы от положения равновесия a (0) под действием постоянного воздействия той же величины, что и амплитуда вынуждающего воздействия. Это утверждение справедливо только при малом затухании. Зависимость называется резонансной кривой (см. рис.7.3.3.).

В установившемся режиме вынужденных колебаний энергия колебательной системы остается неизменной. Система непрерывно поглощает от источника внешнего воздействия энергию, которая восполняет потери, связанные с наличием затухания (сила трения при механических колебаниях, выделение теплоты на активном сопротивлении при колебаниях в контуре).

Найдем среднюю энергию, поглощаемую в единицу времени. Вычисления проведем для пружинного маятника при наличии силы трения и периодически изменяющейся внешней силы. При смещении груза на dx внешняя сила совершит работу Fdx.

Работа, совершенная в единицу времени, будет равна . Среднее значение поглощаемой в единицу времени энергии равно:

. (7.3.9)

Здесь усреднение производится по одному периоду колебаний . Подставляя в интеграл (7.3.9) выражение для силы, и производную от смещения из выражения (7.3.2), получаем

, (7.3.10)

где величина j определяется выражением (7.3.4). После интегрирования находим:

. (7.3.11)

Преобразование с учетом (7.3.4) приводит к выражению:

. (7.3.12)

Учитывая, что , получаем:

. (7.3.13)

Как видно, поглощаемая в единицу времени энергия зависит от частоты W. Так как имеет резонансный пик – максимум, то имеет резонансный пик – минимум (см. рис. 7.3.4) Поэтому измерения зависимости поглощенной энергии от частоты позволяют обнаружить резонансные явления и установить собственные частоты осциллирующих систем.

Переменный ток.

Переме́нный ток — электрический ток, который с течением времени изменяется по величине и направлению или, в частном случае, изменяется по величине, сохраняя своё направление в электрической цепи неизменным.

Переменный ток, текущий через резистор сопротивления, катушку индуктивности, конденсатор. Закон Ома.

Установившиеся вынужденные электромагнитные колебания можно рассматривать как протекание в цепи, содержащей резистор, катушку индуктивности и конденсатор, переменного тока. Переменный ток можно считать квазистационарным, т. е. для него мгновенные значения силы тока во всех сечениях цепи практически одинаковы, таккак их изменения происходят достаточно медленно, а электромагнит­ные возмущения распространяются по цепи со скоростью, равной скорости света. Для мгновенных значений квазистационарных токов выполняются закон Ома и вытека­ющие из него правила Кирхгофа, которые будут использованы применительно к пере­менным токам (эти законы уже использовались при рассмотрении электромагнитных колебаний).

Рассмотрим последовательно процессы, происходящие на участке цепи, содер­жащем резистор, катушку индуктивности и конденсатор, к концам которого приложено переменное напряжение

(149.1)

где U _m — амплитуда напряжения.

1. Переменный ток, текущий через резистор сопротивлением R (L ®0, C ®0) (рис. 213, а). При выполнении условия квазистационарности ток через резистор опреде­ляется законом Ома:

где амплитуда силы тока I _m= U _m /R.

Для наглядного изображения соотношений между переменными токами и напряже­ниями воспользуемся методом векторных диаграмм. На рис. 213, б дана векторная диаграмма амплитудных значений тока I _m и напряжения U _m на резисторе (сдвиг фаз между I _m и U _m равен нулю).

^ 2. Переменный ток, текущий через катушку индуктивностью L (R ®0, C ®0) (рис. 214, а). Если в цепи приложено переменное напряжение (149.1), то в ней потечет переменный ток, в результате чего возникнет э.д.с. самоиндукции (см. (126.3)) . Тогда закон Ома (см. (100.3)) для рассматриваемого участка цепи имеет вид

откуда

(149.2)

Таккак внешнее напряжение приложено к катушке индуктивности, то

(149.3)

есть падение напряжения на катушке. Из уравнения (149.2) следует, что

после интегрирования, учитывая, что постоянная интегрирования равна нулю (так как отсутствует постоянная составляющая тока), получим

(149.4)

где I _m= U _m/(wL). Величина

(149.5)

называется реактивным индуктивным сопротивлением (или индуктивным сопротивлени­ем). Из выражения (149.5) вытекает, что для постоянного тока (w = 0) катушка индук­тивности не имеет сопротивления. Подстановка значения U _m =wLI _m в выражение (149.2) с учетом (149.3) приводит к следующему значению падения напряжения на катушке индуктивности:

(149.6)

Сравнение выражений (149.4) и (149.6) приводит к выводу, что падение напряжения U_L опережает по фазе ток I, текущий через катушку, на p /2, что и показано на векторной диаграмме (рис. 214, б).

^ 3. Переменный ток, текущий через конденсатор емкостью С (R ®0, L ®0) (рис. 215, в). Если переменное напряжение (149.1) приложено к конденсатору, то он все время перезаряжается, и в цепи течет переменный ток. Так как все внешнее напряжение приложено к конденсатору, а сопротивлением подводящих проводов можно пренеб­речь, то

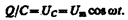
Сила тока

(149.7)

где

Величина

называется реактивным емкостным сопротивлением (или емкостным сопротивлением). Для постоянного тока (w = 0) R_С = ¥, т. е. постоянный ток через конденсатор течь не может. Падение напряжения на конденсаторе

(149.8)

Сравнение выражений (149.7) и (149.8) приводит к выводу, что падение напряжения U_С отстает по фазе от текущего через конденсатор тока I на p /2. Это показано на векторной диаграмме (рис. 215, б).

^ 4. Цепь переменного тока, содержащая последовательно включенные резистор, ка­тушку индуктивности и конденсатор. На рис. 216, а представлен участок цепи, содер­жащий резистор сопротивлением R, катушку индуктивностью L и конденсатор ем­костью С, к концам которого приложено переменное напряжение (149.1). В цепи возникнет переменный ток, который вызовет на всех элементах цепи соответствующие падения напряжения U_R, U_L и U_C. На рис. 216, б представлена векторная диаграмма амплитуд падений напряжений на резисторе (U_R), катушке (U_L) и конденсаторе (U_C). Амплитуда U _m приложенного напряжения должна быть равна векторной сумме амп­литуд этих падений напряжений. Как видно из рис. 216, б, угол j определяет разность фаз между напряжением и силой тока. Из рисунка следует, что (см. также формулу (147.16))

(149.9)

Из прямоугольного треугольника получаем откуда ам­плитуда силы тока имеет значение

(149.10)

совпадающее с (147.15).

Следовательно, если напряжение в цепи изменяется по закону U = U _m cos w t, то в цепи течет ток

(149.11)

где j и I _m определяются соответственно формулами (149.9) и (149.10). Величина

(149.12)

называется полным сопротивлением цепи, а величина

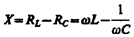
– реактивным сопротивлением.

Рассмотрим частный случай, когда в цепи отсутствует конденсатор. В данном случае падения напряжений U_R и U_L в сумме равны приложенному напряжению U. Векторная диаграмма для данного случая представлена на рис. 217, из которого следует, что

(149.13)

Выражения (149.9) и (149.10) совпадают с (149.13), если в них 1/(wC) = 0, т.е. С =¥. Следовательно, отсутствие конденсатора в цепи означает С =¥, а не С= 0. Данный вывод можно трактовать следующим образом: сближая обкладки конденсатора до их полного соприкосновения, получим цепь, в которой конденсатор отсутствует (расстоя­ние между обкладками стремится к нулю, а емкость — к бесконечности; см. (94.3)).

Явление резонанса.

Поиск по сайту: