Затухание свободных колебаний

- это процесс, в котором одна проведенная реакция вызывает последующие реакции такого же типа.

При делении одного ядра урана образовавшиеся нейтроны могут вызвать деления других ядер урана, при этом число нейтронов нарастает лавинообразно.

Отношение числа образовавшихся нейтронов в одном акте деления к числу таких нейтронов в предыдущем акте деления называется коэффициентом размножения нейтронов k.

При k меньше 1 реакция затухает, т.к. число поглщенных нейтронов больше числа вновь образовавшихся.
При k больше 1 почти мгновенно происходит взрыв.
При k равном 1 идет управляемая стационарная цепная реакция.

Цепная реакция сопровождается выделением большого количества энергии.

Для осуществлении цепной реакции не получается использовать любые ядра, делящиеся под влиянием нейтронов.

Используемый в качестве топлива для атомных реакторов химический элемент уран состоит в природе из двух изотопов: урана-235 и урана - 238.

В природе изотопы урана-235 составляют всего лишь 0,7% от всего запаса урана, однако именно они пригодны для проведения цепной реакции, т.к. делятся под влиянием медленных нейтронов.

Ядра урана-238 могут делиться лишь под влиянием нейтронов большой энергии (быстрых нейтронов). Такую энергию имеют только 60% нейтронов, появляющихся при делении ядра урана-238. Примерно только 1 из 5 образовавшихся нейтронов вызывает деление ядра.

Условия протекания цепной реакции в уране-235:

- минимальное количество топлива (критическая масса), необходимое для проведения управляемой цепной реакции в атомном реакторе
- скорость нейтронов должна вызывать деление ядер урана
- отсутствие примесей, поглощающих нейтроны

Критическая масса:

- если масса урана мала, нейтроны будут вылетать за его пределы, не вступая в реакцию
- если масса урана велика, возможен взрыв за счет сильного увеличения числа нейтронов
- если масса соответствует критической, протекает управляемая цепная реакция

Для урана-235 критическая масса составляет 50 кг (это, например, шар из урана диаметром 9 см).

Первая управляемая цепная реакция - США в 1942 г. (Э.Ферми)
В СССР - 1946 г. (И.В.Курчатов).

12. Понятие о ядерной энергетике.

Ядерная энергетика (Атомная энергетика) — это отрасль энергетики, занимающаяся производством электрической и тепловой энергии путём преобразования ядерной энергии.

Обычно для получения ядерной энергии используют цепную ядерную реакцию деления ядер урана-235 или плутония. Ядра делятся при попадании в них нейтрона, при этом получаются новые нейтроны и осколки деления. Нейтроны деления и осколки деления обладают большой кинетической энергией. В результате столкновений осколков с другими атомами эта кинетическая энергия быстро преобразуется в тепло.

Хотя в любой области энергетики первичным источником является ядерная энергия (например, энергия солнечных ядерных реакций в гидроэлектростанциях и электростанциях, работающих на органическом топливе, энергия радиоактивного распада в геотермальных электростанциях), к ядерной энергетике относится лишь использование управляемых реакций в ядерных реакторах.

Ядерная энергия производится в атомных электрических станциях, используется на атомных ледоколах, атомных подводных лодках; США осуществляют программу по созданию ядерного двигателя для космических кораблей, кроме того, предпринимались попытки создать ядерный двигатель для самолётов (атомолётов) и «атомных» танков.

13. Реакция синтеза атомных ядер.

Но для того, чтобы произошло слияние атомных ядер, их необходимо сблизить на расстояние порядка 10^-13 м, после чего процесс слияния происходит с заметной вероятностью. Отметим, что расстояние 10^-13 м все еще значительно больше расстояния, на котором начинают действовать ядерные силы притяжения.

На рис. 17.4 изображен примерный график зависимости потенциальной энергии взаимодействия двух ядер. На этом рисунке W - относительная кинетическая энергия ядер. Как видно из рисунка, она меньше потенциального барьера, который возникает за счет кулоновского отталкивания двух ядер. Пройти "под барьером" и попасть в глубокую потенциальную яму, возникающую за счет действия ядерных сил притяжения, налетающее ядро может из-за корпускулярно-волнового дуализма микрочастиц (см. лекцию 6).

Рис. 17.4

Волновая функция Ψ налетающего ядра в области потенциального барьера хотя и убывает, но если барьер не очень велик, значение волновой функции за барьером будет заметно отлично от нуля. Как известно, |Ψ(r)|²dV = dV - вероятности обнаружить микрочастицу в объеме dV. Значит, будет отлична от нуля вероятность обнаружить частицу за потенциальным барьером, в области ямы. Этот эффект называется "тунелированием". Именно наличие тунелирования дает вероятность ядрам начать слияние, начиная с расстояний 10^-13 м. "Классическая" частица для попадания в яму должна была бы иметь энергию не меньше высоты потенциального барьера и подходить к своей "партнерше" на расстояние ~ 10^-5 м, где начинают действовать ядерные силы.

Определим W - энергию ядер, необходимую для сближения на расстояние 10^-13 м. Как известно из электростатики (см. Часть 2, (3.3)), потенциальная энергия взаимодействия двух точечных зарядов дается формулой:

Для двух ядер дейтерия, например, q₁=q₂=e=1,6·10^-19 Кл. При r=10^-13 м имеем:

Сообщить ядрам такую энергию можно разогрев вещество до очень высокой температуры. Температуру оценим, приравнивая эту энергию средней энергии теплового движения, равную (3/2)kT, где k=1,38·10^-23 Дж/К:

В земных условиях реакции синтеза легких ядер впервые были реализованы в виде термоядерного взрыва (в так называемой водородной бомбе). Высокая температура, необходимая для протекания реакции синтеза в водородной бомбе, создается за счет взрыва ядерной бомбы, служащей в водородной бомбе детонатором, "поджигателем" термоядерного взрыва. В водородной бомбе используются реакции синтеза:

В реакциях (17.2) и (17.3) образуется дорогостоящий тритий, который и вступает в реакцию с дейтерием (17.1). Образующиеся в реакциях (17.1) нейтроны имеют энергию 14 МэВ, поэтому могут вызывать деление ядер, который составляет более 99% природного урана. Для усиления энергии взрыва, бомбу окружают оболочкой из природного урана. Энергия взрыва термоядерных бомб на 2-3 порядка выше, чем ядерных и составляет от 100000 до 1000000 тонн тротила.

Управляемый термоядерный синтез, проходящий в регулируемых условиях, пока еще не реализован.

Наиболее перспективной реакцией для управляемого термоядерного синтеза является реакция (17.1), так как она протекает с наибольшей скоростью.

При температурах Т~10⁸ К, необходимых для протекания реакции синтеза, вещество ионизируется: ядра и электроны уже не связаны друг с другом: вещество переходит в состояние полностью ионизированной плазмы. Основная проблема состоит в том, как удержать горячую плазму в зоне реакции. Одним из основных направлений решения этой проблемы является создание установок, в которых плазма удерживается с помощью магнитного поля. Эту идею в 1950 году высказали советские ученые И.Е. Тамм и А.Д. Сахаров. Она реализуется различными способами, но наибольшие усилия были затрачены на создание устройств, которые получили название "ТОКОМАК". Это название является сокращением от полного названия: "тороидальная камера с магнитными катушками". В настоящее время работы на токомаках переходят из фазы чисто физических исследований в фазу создания экспериментального термоядерного реактора. Существует международный проект, который предполагается осуществить к 2003 году и который должен служить экспериментальной моделью будущей электростанции с реакцией синтеза на основе токомака.

В заключении отметим, что системы с магнитным удержанием плазмы - не единственный путь к реализации управляемой реакции синтеза. С 1964 года начались исследования в области управляемого термоядерного синтеза с применением лазерного нагрева. При этом термоядерное горючее имеет вид небольших крупинок, диаметром несколько миллиметров, состоящих из дейтерий-тритиевого льда. Лазерное излучение фокусируется на этой мишени и разогревает ее до термоядерных температур Работа подобного реактора может осуществляться только в импульсном режиме. Пока эти исследования далеки до завершения.

Исключительная важность для всего человечества решения проблемы управляемой термоядерной реакции состоит в том, что запасы традиционных источников энергии (нефть, газ, уголь) стремительно истощаются и управляемые термоядерные реакции должны стать основой энергетики будущего.

Затухание свободных колебаний

Затуханием колебаний называется постепенное ослабление колебаний с течением времени, обусловленное потерей энергии колебательной системой. Закон затухания колебаний зависит от свойств колебательной системы. Система называется линейной, если параметры, характеризующие существенные в рассматриваемом процессе физические свойства системы, не изменяются в ходе процесса. Свободные затухающие колебания линейной системы описываются уравнением:

, (7.1.1)

где - коэффициент затухания, - собственная частота системы, т.е. частота, с которой совершались бы колебания в отсутствии затухания. Выражение коэффициента затухания через параметры системы зависит от вида колебательной системы. Например, для пружинного маятника где r - коэффициент сопротивления, т.е. коэффициент пропорциональности между скоростью и силой сопротивления. Для затухающих колебаний в колебательном контуре (рис.7.1.1): 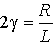, где R - величина активного сопротивления контура.

Для решения уравнения (7.1.1) производится подстановка . Эта подстановка приводит к характеристическому уравнению:

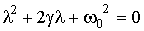, (7.1.2)

которое имеет два корня:

, . (7.1.3)

При не слишком большом затухании (при ) подкоренное выражение будет отрицательным. Если его представить в виде , где - вещественная положительная величина, называемая циклической частотой затухающих колебаний и равная , то корни уравнения (3) запишутся в виде:

и . (7.1.4)

Общим решением уравнения (7.1.1) будет функция:

(7.1.5)

которую можно представить в виде:

, (7.1.6)

Здесь и - произвольные постоянные.

В соответствии с (7.1.6) движение системы можно условно рассматривать как гармоническое колебание частоты w с амплитудой, изменяющейся по закону:

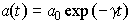. (7.1.7)

Скорость затухания колебаний определяется коэффициентом затухания 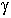. В соответствии с выражением (7.1.7) коэффициент затухания обратен по величине тому промежутку времени, за который амплитуда колебаний уменьшается в «e»=2.718 раз. Период затухающих колебаний определяется формулой:

. (7.1.8)

При незначительном затухании ( ) период колебаний практически равен . С ростом период увеличивается. Из соотношения (7.1.7) следует, что . Такое отношение амплитуд называется декрементом затухания, а его натуральный логарифм - логарифмическим декрементом затухания:

. (7.1.9)

Логарифмический декремент затухания обратен по величине числу колебаний, совершаемых за то время, за которое амплитуда уменьшается в «e» раз. Помимо рассмотренных величин для характеристики колебательной системы употребляется величина , называемая добротностью колебательной системы. Добротность пропорциональна числу колебаний, совершаемых системой за то время, за которое амплитуда колебаний уменьшается в «e» раз. Большим значениям добротности соответствует малое затухание. Энергия колебательной системы убывает со временем. Это обусловлено наличием затухания. При малом затухании, когда энергия изменяется по закону:

, (7.1.10)

где - значение энергии в начальный момент.

Можно показать, что при слабом затухании добротность с точностью до множителя 2p равна отношению энергии, запасенной в системе в данный момент времени, к убыли этой энергии за один период колебаний.

С ростом g период колебаний увеличивается. При период обращается в бесконечность, т.е. движение перестает быть периодическим. При 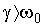выведенная из положения равновесия система возвращается в него, не совершая колебаний.

Поиск по сайту: