 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Резонанс токов
Рассмотрим цепь переменного тока, содержащую параллельно включенные конденсатор емкостью С и катушку индуктивностью L (рис. 219). Для простоты допустим, что активное сопротивление обеих ветвей настолько мало, что им можно пренебречь. Если приложенное напряжение изменяется по закону U= U m сos w t (см. (149.1)), то, согласно формуле (149.11),в ветви 1С2 течет ток
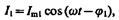
амплитуда которого определяется из выражения (149.10) при условии R= 0 и L =0:
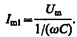

Начальная фаза j 1 этого тока по формуле (149.9) определяется равенством
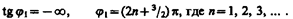 (151.1)
(151.1)
Аналогично, сила тока в ветви 1L2

амплитуда которого определяется из (149.10) при условии R= 0 и С =¥ (условие отсутствия емкости в цепи, см. § 149):

Начальная фаза j 2 этого тока (см. (149.9))
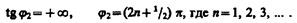 (151.2)
(151.2)
Из сравнения выражений (151.1) и (151.2) вытекает, что разность фаз токов в ветвях 1С2 н 1L2 равна j 1 —j 2 =p, т. е. токи в ветвях противоположны по фазе. Амплитуда силы тока во внешней (неразветвленной) цепи

Если w = w рез = 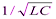 , то I m1= I m2и I m=0. Явление резкого уменьшения амплитуды силы тока во внешней цепи, питающей параллельно включенные конденсатор и катушку индуктивности, при приближении частоты w приложенного напряжения к резонансной частоте w рез называется резонансом токов (параллельным резонансом). В данном случае для резонансной частоты получили такое же значение, как и при резонансе напряжений (см. § 150).
, то I m1= I m2и I m=0. Явление резкого уменьшения амплитуды силы тока во внешней цепи, питающей параллельно включенные конденсатор и катушку индуктивности, при приближении частоты w приложенного напряжения к резонансной частоте w рез называется резонансом токов (параллельным резонансом). В данном случае для резонансной частоты получили такое же значение, как и при резонансе напряжений (см. § 150).
Амплитуда силы тока ^ I m оказалась равна нулю потому, что активным сопротивлением контура пренебрегли. Если учесть сопротивление R, то разность фаз j 1 —j 2будет равна p, поэтому при резонансе токов амплитуда силы тока I mбудет отлична от нуля, но примет наименьшее возможное значение. Таким образом, при резонансе токов во внешней цепи токи I 1 и I 2 компенсируются и сила тока I в подводящих проводах достигает минимального значения, обусловленного только током через резистор. При резонансе токов силы токов I 1 и I 2 могут значительно превышать силу тока I.
Рассмотренный контур оказывает большое сопротивление переменному току с частотой, близкой к резонансной. Поэтому это свойство резонанса токов используется в резонансных усилителях, позволяющих выделять одно определенное колебание из сигнала сложной формы. Кроме того, резонанс токов используется в индукционных печах, где нагревание металлов производится вихревыми токами (см. § 125). В них емкость конденсатора, включенного параллельно нагревательной катушке, подбирается так, чтобы при частоте генератора получился резонанс токов, в результате чего сила тока через нагревательную катушку будет гораздо больше, чем сила тока в подводящих проводах.
Упругие волны. Поперечные и продольные волны.
Упругая волна
Если тело находится в упругой среде, то колебательное движение деформирует эту среду. Из-за взаимодействия соседних частиц среды деформация передается от одних участков к другим. Это и есть волна. Например, волна на озере, если бросить камень: камень вызывает деформацию, которая распространяется в упругой среде - воде.
Виды волн
Волны могут быть поперечными и продольными. Представим распространение волн с помощью модели, в которой частицы среды представлена в виде совокупности шариков и пружинок.
В продольных волнах шарики испытывают смещение вдоль цепочки, а пружинки растягиваются или сжимаются. В жидкостях или газах деформация такого рода сопровождается уплотнением или разрежением. Такие волны могут распространятся в любых средах - твердых, жидких и газообразных.

Если один или несколько шариков сместятся в направлении, перпендикулярном цепочке, то возникает деформация сдвига. В результате вдоль цепочки побежит поперечная волна. Поперечные волны могут существовать только в твердых телах.

Характеристики волны
Длина волны - это расстояние между двумя ближайшими горбами или впадинами поперечной волны, или расстояние между двумя ближайшими сгущениями или разрежениями продольной волны.
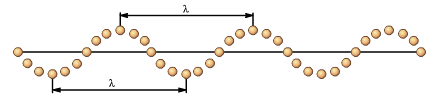
Скорость волны - это скорость распространения колебаний.
Скорость распространения волны и длина волны зависят от среды, в которой они распространяются. Наибольшая скорость распространения волн в твердых телах, наименьшая - в газах.
Длина волны. Уравнение плоской бегущей волны.
Уравнение плоской одномерной синусоидальной волны:
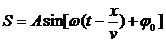
(Вместо синуса можно написать косинус.) Это уравнение отличается от уравнения синусоидальных колебаний тем, что колеблющая величина S зависит не только от времени, но и от координаты. Это и понятно: вместо одного маятника мы имеем множество связанных маятников - частиц среды. v - скорость распространения волны, А - амплитуда волны, аргумент синуса - фаза волны, j0 - начальная фаза колебаний в точке х = 0, w - частота (циклическая) волны.
Расстояние, на которое распространяется волна за время, равное периоду колебаний, называется ДЛИНОЙ ВОЛНЫ l = nT.
ВОЛНОВОЕ ЧИСЛО k:
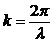
С помощью введенного волнового числа уравнение волны запишется:

Если мы рассматриваем не одномерную волну, удобно наряду с волновым числом ввести ВОЛНОВОЙ ВЕКТОР k, модуль которого равен волновому числу, а направление совпадает с направлением луча (направлением распространения волны). В векторном виде уравнение волны будет выглядеть так:
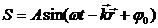
здесь r - радиус вектор точки пространства; j0 - начальная фаза колебаний в начале координат.
Уравнение сферической волны отличается тем, что амплитуда волны убывает с расстоянием от источника:
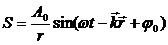
A 0 = const по смыслу формулы есть амплитуда волны на единичном расстоянии от источника.
Уравнение волны в дифференциальной форме обычно называют волновым уравнением; вид этого уравнения следующий:
 или
или 
| Здесь D S - оператор |
|
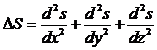
Уравнение синусоидальной волны является решением волнового уравнения (можно проверить подстановкой). Общее же решение волнового уравнения следующее:
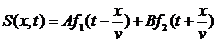
Здесь А и В - произвольные константы, а f1 и f2 - произвольные дважды дифференцируемые функции. Первое слагаемое описывает волну, распространяющуюся слева направо, второе - встречную волну.
Звук.
Звуковыми волнами или просто звуком принято называть волны, воспринимаемые человеческим ухом. Диапазон звуковых частот лежит в пределах приблизительно от 20 Гц до 20 кГц. Волны с частотой менее 20 Гц называются инфразвуком, а с частотой более 20 кГц – ультразвуком. Волны звукового диапазона могут распространяться не только в газе, но и в жидкости (продольные волны) и в твердом теле (продольные и поперечные волны). Однако волны в газообразной среде – среде нашего обитания – представляют особый интерес.
Изучением звуковых явлений занимается раздел физики, который называют акустикой. При распространении звука в газе атомы и молекулы колеблются вдоль направления распространения волны. Это приводит к изменениям локальной плотности ρ и давления p. Звуковые волны в газе часто называют волнами плотности или волнами давления. В простых гармонических звуковых волнах, распространяющихся вдоль оси OX, изменение давления p(x, t) зависит от координаты x и времени t по закону
Электромагнитная волна (определение свойства и получение).
Волна́ — изменение некоторой совокупности физических величин (характеристик некоторого физического поля или материальной среды), которое способно перемещаться, удаляясь от места их возникновения, или колебаться внутри ограниченных областей пространства.
Волны могут генерироваться различными способами.
· Генерация локализованным источником колебаний (излучателем, антенной).
· Спонтанная генерация волн в объёме при возникновении гидродинамических неустойчивостей. Такую природу могут иметь, например, волны на воде при достаточно большой скорости ветра, дующего над водной гладью.
· Переход волн одного типа в волны другого типа. Например, при распространении электромагнитных волн в кристаллическом твёрдом теле могут генерироваться звуковые волны.
Резонансные явления [править | править исходный текст]
В ограниченных в пространстве субстанциях волновым процессам свойственно проявление резонансных эффектов, обусловленных множественным наложением прямых и отражённых от границ волн, что приводит к резкому возрастанию амплитуды волнового процесса. При множественном наложении в области резонанса происходит аддитивное накопление энергии динамической системой вследствие синфазности прямых и обратных волн. Обычно принято считать, что в идеальных динамических системах без диссипации энергии при частоте резонанса амплитуда колебаний становится бесконечной, но это не всегда происходит, поскольку энергия свободных колебаний во многих случаях остаётся конечной. Здесь следует различать особенности возникновения резонансов в динамических системах:
· Резонансные явления различаются в зависимости от того, являются ли волновые процессы вынужденными или свободными.
Вынужденные процессы возникают в системе при постоянном динамическом воздействии внешней силы. В этом случае спектр колебаний, возникающих в системе, является непрерывным с возрастанием амплитуды на резонансных частотах.
Расчетная амплитудно-частотная (а) и фазо-частотная (б) характеристики входного сопротивления 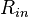 при различных значениях активной нагрузки
при различных значениях активной нагрузки  и постоянной величине амплитуды входного тока
и постоянной величине амплитуды входного тока  от частоты.
от частоты.
На графиках мы видим, что при определенной нагрузке графики амплитуды и фазы становятся монотонными (красная линия), что свидетельствует об отсутствии отражения от конца линии, и линия ведёт себя как бесконечная. Вынужденные волновые процессы описываются волновым уравнением (системой уравнений для динамических систем с сосредоточенными параметрами) с правой частью, в которую подставляется значение воздействующей внешней силы. В математике такого типа уравнения называются неоднородными, а их решения называют частными решениями [6]
Свободные колебания являются результатом последействия после окончания воздействия внешнего возмущения. Для этих волновых процессов характерен дискретный спектр, соответствующий частотам внутренних резонансов динамической системы. Данные колебания описываются волновым уравнением (системой уравнений) с нулевой правой частью. В математике такого типа дифференциальные уравнения называют однородными, а их решения – общими. Для нахождения постоянных интегрирования в данном случае требуется знание ненулевых параметров колебания хотя бы в одной точке динамической системы. При нулевом отклонении параметров всей системы (отсутствии предварительного возмущения) общее решение уравнения будет обращаться в ноль. При этом частное решение может быть и ненулевым. Таким образом, общее и частное решение волнового уравнения описывают различные процессы, возникающие в динамической системе. Частное решение описывает реакцию на непосредственное воздействие на систему, а общее решение – последействие системы при окончании воздействия на неё.
· Резонансные явления различаются в зависимости от дискретности или непрерывности самой динамической системы. В динамической системе с сосредоточенными параметрами резонансные явления даже в случае идеальности самой системы не приводят к бесконечному возрастанию амплитуды колебаний.
При предельном переходе к динамической системе с распределёнными параметрами в идеальном случае амплитуды возрастают до бесконечности. В линиях с сопротивлением, амплитуды резонансов в любом случае конечны. Величина сопротивления/вязкости влияет как на амплитуды резонансов, уменьшая их, так и смещает частоты резонансов.
· На резонансные явления оказывают влияние условия отражения волны на границах. Ранее мы видели, что при определённых условиях отражения от границы, конечная динамическая система ведёт себя как бесконечная. При неполном отражении от границы возникают совместные стоячие и прогрессивные волны, описываемые коэффициентом стоячей волны.
Если волновое сопротивление границы (в динамических системах с сосредоточенными параметрами) носит комплексный характер, то при определённых значениях такого сопротивления в динамической системе происходит резкое смещение резонансных частот.
Расчётная амплитудно-частотная (а) и фазо-частотная (b) характеристики входного сопротивления 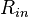 от частоты при различной ёмкости нагрузки
от частоты при различной ёмкости нагрузки 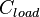 и постоянной величине амплитуды входного тока
и постоянной величине амплитуды входного тока  .
.
· На резонансные процессы влияют и свойства самой динамической системы. В частности, в дискретных динамических системах с резонансными подсистемами возникает четвёртый, резонансный тип колебаний, названный экспериментально открывшим его проф. Скучиком «колебания с отрицательной мерой инерции», поскольку при этих колебаниях входное сопротивление системы становится отрицательным. Это означает, что элемент, на который воздействует внешняя сила, движется встречно направлению воздействия последней. В этом режиме амплитуды колебаний даже в дискретных динамических системах обращаются в бесконечность, и резонансы возникают как выше, так и ниже частотного диапазона резонансов основной динамической системы.
Динамические системы с сосредоточенными параметрами можно рассматривать как динамические системы с распределёнными параметрами при условии:

где 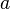 – расстояние между элементами динамической системы с сосредоточенными параметрами.
– расстояние между элементами динамической системы с сосредоточенными параметрами.
· Наконец, на резонансные вынужденные колебания в динамической системе влияет точка приложения внешней силы. При определённом положении резонансы могут возникать только в части динамической системы.
Диаграммы вынужденных колебаний в конечной однородной упругой линии с незакрепленными концами при воздействии внешней силы на внутренние элементы линии.
Причём указанная особенность проявляется и в апериодическом режиме колебаний.
Диапазоны электромагнитных волн.
Электромагнитное излучение принято делить по частотным диапазонам (см. таблицу). Между диапазонами нет резких переходов, они иногда перекрываются, а границы между ними условны. Поскольку скорость распространения излучения (в вакууме) постоянна, то частота его колебаний жёстко связана с длиной волны в вакууме.
| Название диапазона | Длины волн, λ | Частоты, ν | Источники | |
| Радиоволны | Сверхдлинные | более 10 км | менее 30 кГц | Атмосферные имагнитосферныеявления. Радиосвязь. |
| Длинные | 10 км — 1 км | 30 кГц — 300 кГц | ||
| Средние | 1 км — 100 м | 300 кГц — 3 МГц | ||
| Короткие | 100 м — 10 м | 3 МГц — 30 МГц | ||
| Ультракороткие | 10 м — 1 мм | 30 МГц — 300 ГГц[4] | ||
| Инфракрасное излучение | 1 мм — 780 нм | 300 ГГц — 429 ТГц | Излучение молекул и атомов при тепловых и электрических воздействиях. | |
| Видимое излучение | 780—380 нм | 429 ТГц — 750 ТГц | ||
| Ультрафиолетовое | 380 — 10 нм | 7,5·1014 Гц — 3·1016 Гц | Излучение атомов под воздействием ускоренных электронов. | |
| Рентгеновские | 10 нм — 5 пм | 3·1016 — 6·1019 Гц | Атомные процессы при воздействии ускоренных заряженных частиц. | |
| Гамма | менее 5 пм | более 6·1019 Гц | Ядерные и космические процессы, радиоактивный распад. |
Радиоволны. Ультракороткие радиоволны принято разделять на метровые, дециметровые, сантиметровые, миллиметровые и субмиллиметровые (микрометровые). Волны с длиной λ < 1 м (ν > 300 МГц) принято также называть микроволнами или волнами сверхвысоких частот (СВЧ).
Ионизирующее электромагнитное излучение. К этой группе традиционно относят рентгеновское и гамма-излучение, хотя, строго говоря, ионизировать атомы может и ультрафиолетовое излучение, и даже видимый свет. Границы областей рентгеновского и гамма-излучения могут быть определены лишь весьма условно. Для общей ориентировки можно принять, что энергия рентгеновских квантов лежит в пределах 20 эВ — 0,1 МэВ, а энергия гамма-квантов — больше 0,1 МэВ. В узком смысле гамма-излучение испускается ядром, а рентгеновское — атомной электронной оболочкой при выбивании электрона с низколежащих орбит, хотя эта классификация неприменима к жёсткому излучению, генерируемому без участия атомов и ядер (например, синхротронному или тормозному излучению).
Поиск по сайту:
