Анализ сезонных колебаний

В рядах динамики, уровни которых являются месячными или квартальными показателями, наряду со случайными колебаниями часто наблюдаются сезонные колебания, под которыми понимаются периодически повторяющиеся из года в год повышение и снижение уровней в отдельные месяцы или кварталы.

Сезонным колебаниям подвержены внутригодовые уровни многих показателей. Например, расход электроэнергии в летние месяцы значительно меньше, чем в зимние; или рыночные цены на овощи в отдельные месяцы далеко не одинаковы.

При графическом изображении таких рядов сезонные колебания проявляются в повышении и снижении уровней в определенные месяцы (кварталы). В качестве иллюстрации рядов с сезонными колебаниями могут служить данные, представленные в табл. 32 и их графическое изображение (рис. 15).

Таблица 32. Динамика производства мороженого предприятием по месяцам, тонн

Номер строки	Год	Месяц t
январь	февраль	март	апрель	май	июнь	июль	август	сентябрь	октябрь	ноябрь	декабрь
	Итого
		33,333	38,000	43,667	54,333	55,333	69,000	64,667	52,000	42,333	36,000	33,333	31,333
		0,723	0,824	0,947	1,178	1,200	1,496	1,402	1,128	0,918	0,781	0,723	0,680

Рис. 15. Динамика производства мороженого предприятием по месяцам, тонн

Вместо месячных показателей могут быть квартальные. Если колебания не случайны, то они сохраняются и в квартальных уровнях, как это показано в табл. 33 и на рис. 16, где месячные данные из табл. 32 преобразованы в квартальные.

Таблица 33. Динамика производства мороженого предприятием по кварталам, тонн

Рис. 16. Динамика производства мороженого предприятием по кварталам, тонн

Наблюдение за сезонными колебаниями позволяет устранить их там, где они нежелательны, а также решить ряд практических задач, например, определить потребности в сырье, рабочей силе в тех отраслях, где влияние сезонности велико.

При изучении рядов динамики, содержащих «сезонную волну», ее выделяют из общей колеблемости уровней и измеряют. Существует 2 основных метода для решения этой задачи: расчет индексов сезонности и гармонический анализ.

Индексы сезонности показывают, во сколько раз фактический уровень ряда в определенный момент или интервал времени t больше среднего уровня, либо уровня, вычисляемого по уравнению тренда (). Способы расчета индексов сезонности зависят от наличия или отсутствия тренда. Если тренда нет или от незначителен, то для каждого месяца (квартала) индекс сезонности определяется по формуле (106):

, (106)

где Y_t – уровень ряда динамики за месяц (квартал) t;

– средний уровень всего ряда динамики.

Индексы сезонности желательно рассчитывать для рядов динамики, длиной в несколько лет, тогда формула индекса сезонности примет следующий вид:

, (107)

где – средний уровень ряда динамики по одноименным месяцам t за T лет.

Например, по данным таблицы 32, представляющим ряд динамики за 3 года, индексы сезонности будем рассчитывать по формуле (107), для чего сначала рассчитаем (4-я строка таблицы 32), а затем, разделив полученные значение на T =3, получим средние уровни за каждый месяц (5-я строка таблицы 32). Средний уровень всего ряда определяем по формуле средней арифметической простой: . В 6-й строке таблицы 32 определены индексы сезонности для каждого месяца по формуле (107), то есть делением значений в 5-й строке на 46,111.

При наличии тренда индексы сезонности определяются определяются аналогично по формулам (106) – (107) с учетом замены на выравненные по уравнению тренда уровни . На основе найденных индексов сезонности и тренда можно спрогнозировать (экстраполировать) ряд динамики по формуле:

. (108)

Особое место при анализе сезонных колебаний занимает гармонический анализ сезонных колебаний, в котором осуществляется выравнивание ряда динамики с помощью ряда Фурье, уровни которого можно выразить как функцию времени следующим уравнением:

. (109)

То есть сезонные колебания уровней динамического ряда можно представить в виде синусоидальных колебаний. Поскольку последние представляют собой гармонические колебания, то синусоиды, полученные при выравнивании по ряду Фурье, называют гармониками различных порядков (показатель k в этом уравнении определяет число гармоник). Обычно при выравнивании по ряду Фурье рассчитывают несколько гармоник (чаще не более 4) и затем уже определяют, с каким числом гармоник ряд Фурье наилучшим образом отражает изменения уровней ряда.

При выравнивании по ряду Фурье периодические колебания уровней динамического ряда представлены в виде суммы нескольких синусоид (гармоник), наложенных друг на друга.

Так, при k=1 ряд Фурье будет иметь вид

, (110)

а при k=2, соответственно,

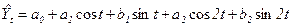(111)

и так далее.

Параметры уравнения теоретических уровней, определяемого рядом Фурье, находят, как и в других случаях, методом наименьших квадратов. Приведем без вывода формулы[36], используемые для исчисления параметров ряда Фурье:

; ; . (112)

Последовательные значения t обычно определяются от 0 с увеличением (приростом), равным , где n – число уровней эмпирического ряда.

Например, при n=10 временнЫе точки t можно записать следующим образом:

,

или (после сокращения): ; ; ; ; ; ; ; ; .

При n=12 значения t приведены в первой строке таблицы 34, а во второй и третьей строках определены значения sin kt и cos kt для первой гармоники.

Таблица 34. Значения sin kt и cos kt для первой гармоники 12-ти уровнего ряда динамики

t

p/6

p/3

p/2

2p/3

5p/6

p

7p/6

4p/3

3p/2

5p/3

11p/6

cost

–

–

–1

–

–

sint

–

–

–1

–

–

В таблице 35 приведены исходные данные (графы 1 и 2) и расчет показателей, необходимых для получения уравнений первой гармоники (k=1) по формуле (112).

Таблица 35. Вспомогательные расчеты параметров ряда Фурье

Год		Месяц (t)	Итого
январь (0)	февраль (p/6)	март (p/3)	апрель (p/2)	май (2p/3)	июнь (5p/6)	июль (p)	август (7p/6)	сентябрь (4p/3)	октябрь (3p/2)	ноябрь (5p/3)	декабрь (11p/6)
	y
ycost		30,31	22,5		-29	-55,4	-69	-45	-21	-0	16,5	26,85
ysint		17,5	38,97		50,23			-26	-36,4	-35	-28,6	-15,5
	31,71	37,84	46,18	54,51	60,58	62,78	60,51	54,39	46,04	37,72	31,64	29,44
	y
ycost		34,64			-23	-60,6	-60	-41,6	-23	-0		30,31
ysint			38,11		39,84			-24	-39,8	-38	-31,2	-17,5
	31,71	37,84	46,18	54,51	60,58	62,78	60,51	54,39	46,04	37,72	31,64	29,44
	y
ycost		33,77			-31	-63,2	-65	-48,5	-19,5	-0	15,5	24,25	-259,234
ysint		19,5	36,37		53,69	36,5		-28	-33,8	-35	-26,8	-14	151,122
	31,71	37,84	46,18	54,51	60,58	62,78	60,51	54,39	46,04	37,72	31,64	29,44

Искомое уравнение первой гармоники имеет вид: = 46,111–14,402cos t + 8,396sin t, подстановкой в которое значений t в последней строке табл.35 получены теоретические значения объема производства мороженого по месяцам, а на рис.17 приведено графическое изображение, из которого видно, что различия эмпирических и теоретических уровней незначительны.

Рис. 17. Динамика производства мороженого предприятием, тонн

Аналогично рассчитываются параметры уравнения с применением второй, третьей и т.д. гармоник[37], а затем выбирается наиболее адекватное уравнение, то есть с минимальной ошибкой аппроксимации.

На основе подобранного уравнения по ряду Фурье можно прогнозировать (экстраполировать) развитие уровней ряда в будущем по формуле (104). Например, определим доверительные интервалы производства мороженого на январь 2007 года с вероятностью 0,95, для чего найдем ошибку аппроксимации по формуле (105): 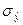= = 4,727 и определим коэффициент доверия по нормальному распределению (так как число уровней n >30) по Приложению 1: t = 1,96. Тогда прогноз на январь 2007 года с вероятностью 0,95 по формуле (104): Y_янв07 = 31,71 1,99*4,727 или 22,44< Y₂₀₀₇ <40,974 (т).

Поиск по сайту: