Вопрос№8 Магнитное поле параллельных токов. Сила ампера. Магнитный поток

Зако́н Ампе́ра — закон взаимодействия электрических токов. Впервые был установлен Андре Мари Ампером в 1820 для постоянного тока. Из закона Ампера следует, что параллельные проводники с электрическими токами, текущими в одном направлении, притягиваются, а в противоположных — отталкиваются. Законом Ампера называется также закон, определяющий силу, с которой магнитное поле действует на малый отрезок проводника с током. Выражение для силы , с которой магнитное поле действует на элемент объёма 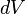проводника с током плотности , находящегося в магнитном поле с индукцией , в Международной системе единиц (СИ) имеет вид:

.

Если ток течёт по тонкому проводнику, то , где — «элемент длины» проводника — вектор, по модулю равный и совпадающий по направлению с током. Тогда предыдущее равенство можно переписать следующим образом:
Направление силы определяется по правилу вычисления векторного произведения, которое удобно запомнить при помощи правила левой руки.

Модуль силы Ампера можно найти по формуле:

где — угол между векторами магнитной индукции и тока.

Сила максимальна когда элемент проводника с током расположен перпендикулярно линиям магнитной индукции ():

Содержание

[убрать]

1 Два параллельных проводника

2 Проявления

3 Применение

4 Примечания

5 См. также

Два параллельных проводника[править | править исходный текст]

Два бесконечных параллельных проводника в вакууме

Наиболее известным примером, иллюстрирующим силу Ампера, является следующая задача. В вакууме на расстоянии друг от друга расположены два бесконечных параллельных проводника, в которых в одном направлении текут токи и . Требуется найти силу, действующую на единицу длины проводника.

В соответствии с законом Био — Савара — Лапласа бесконечный проводник с током в точке на расстоянии создаёт магнитное поле с индукцией

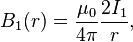
где — магнитная постоянная.

Теперь по закону Ампера найдём силу, с которой первый проводник действует на второй:

По правилу буравчика, направлена в сторону первого проводника (аналогично и для , а значит, проводники притягиваются).

Модуль данной силы ( — расстояние между проводниками):

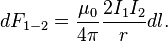
Интегрируем, учитывая только проводник единичной длины (пределы 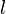от 0 до 1):

Полученная формула используется в СИ для установления численного значения магнитной постоянной . Действительно, ампер, являющийся одной из основных единиц СИ, определяется в ней как «сила неизменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малой площади кругового поперечного сечения, расположенным в вакууме на расстоянии1 метр один от другого, вызвал бы на каждом участке проводника длиной 1 метр силу взаимодействия, равную 2·10⁻⁷ ньютона»^[1].

Таким образом, из полученной формулы и определения ампера следует, что магнитная постоянная равна Н/А² или, что то же самое, Гн/ м точно.

Магнитное поле, какими бы источниками — катушками с током или постоянными магнитами — оно ни создавалось, проявляет себя прежде всего в механическом действии на движущиеся заряды и на проводники с током.

Сила Ампера. Рассмотрим сначала силу, действующую на проводник с током, находящийся в магнитном поле — силу Ампера. Ее существование можно продемонстрировать простым опытом, схема которого показана на рис. 100. Направление силы Ампера соответствует правилу левой руки: когда магнитные силовые линии входят в ладонь, а четыре выпрямленных пальца указывают направление тока, отставленный в сторону большой палец указывает направление силы.

Рис. 100. Обнаружение силы, действующей на проводник с током в магнитном поле

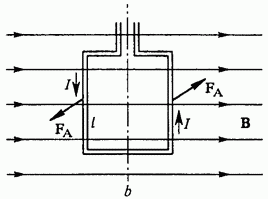
Рис. 101. К выводу выражения для силы Ампера

Именно на использовании этой силы основано действие электроизмерительных приборов магнитоэлектрической системы.

Сила Ампера тем больше, чем больше сила тока в проводнике и чем больше индукция магнитного поля. Выражение для этой силы можно получить с помощью формулы (2) § 15, определяющей индукцию магнитного поля через максимальное значение вращающего момента, действующего на рамку с током в однородном магнитном

поле. Этот момент обусловлен действующими на стороны рамки силами Ампера. Когда рамка расположена так, как показано на рис. 101 (т. е. магнитные силовые линии параллельны ее плоскости), силы действуют только на ее вертикальные стороны, так как горизонтальные стороны направлены вдоль силовых линий.

Силы Ампера действующие на вертикальные стороны рамки, одинаковы и направлены в противоположные стороны, т. е. образуют пару, момент которой равен произведению одной из них на плечо

При указанной ориентации рамки этот момент сил максимален и в соответствии с формулой (2) § 15 равен

Приравнивая правые части (1) и (2), получаем выражение для силы Ампера, действующей на проводник длиной с током расположенный перпендикулярно силовым линиям магнитного поля с индукцией

Эта формула записана в СИ, где сила тока измеряется в амперах, индукция магнитного поля — в тесла, длина — в метрах. Значение силы получается в ньютонах.

Если проводник с током расположен под углом а к вектору В, то вклад в силу Ампера дает только составляющая магнитного поля, перпендикулярная проводнику. В этом случае выражение для силы Ампера записывается в виде

Выражение для вектора силы, действующей на элемент проводника, можно записать, используя векторное произведение:

Зная силу действующую на отдельный элемент проводника с током, можно найти силу, действующую на весь проводник.

Взаимодействие двух параллельных токов. В качестве примера рассмотрим силу взаимодействия двух бесконечных параллельных проводников, по которым идут токи (рис. 102). Будем искать силу, действующую на проводник 1 в магнитном поле, создаваемом проводником 2. Индукция этого магнитного поля выражается формулой (6) § 15, в которую в качестве следует подставить ток в проводнике 2, а в качестве — расстояние между проводниками:

Кольцевые магнитные силовые линии этого поля перпендикулярны проводнику У, поэтому в соответствии с формулой (3) действующая

на его участок длиной сила Ампера равна

Если рассмотреть силу, действующую на проводник 2 в магнитном поле, создаваемом проводником 1, то получится тот же самый результат (7). Когда токи текут в проводниках в одном направлении, эти проводники притягиваются, когда в противоположных направлениях — отталкиваются.

Рис. 102. Взаимодействие двух параллельных проводников с токами

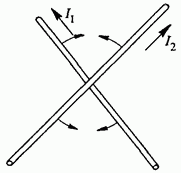
Рис. 103. Взаимодействие двух скрещенных прямолинейных токов

Обратим внимание, что сила, действующая на участок одного проводника в магнитном поле другого проводника, обратно пропорциональна расстоянию между ними.

Если токи текут по двум скрещенным прямым проводам (рис. 103), то между токами действуют силы, стремящиеся повернуть проводники так, чтобы они встали параллельно друг другу и чтобы токи в них текли в одну сторону.

Полная магнитная сила, действующая на ток. При расчете полной силы Ампера, действующей на малый участок бесконечного тонкого проводника с током (как прямого, так и криволинейного), ситуация во многом аналогична той, с которой мы сталкивались в электростатике при нахождении силы, действующей на малый участок поверхности заряженного проводника. Как и в электростатике, здесь необходимо учитывать поле (в данном случае магнитное), создаваемое как всеми другими источниками (другими токами, постоянными магнитами и т.д.), так и всеми остальными участками рассматриваемого проводника с током, кроме выделенного, для которого мы рассчитываем действующую силу.

Для бесконечного прямолинейного тонкого проводника с током подобный эффект «самодействия» отсутствует, так как в соответствии с законом Био—Савара—Лапласа любой его участок не создает магнитного поля в точках, где расположены другие участки этого тонкого проводника. Для изогнутого тонкого проводника, например

кольца с током, ситуация уже иная, так как на отдельный участок уже будут действовать силы со стороны магнитного поля, создаваемого другими участками проводника.

В случае «толстого» проводника (имеющего конечное поперечное сечение) магнитные силы «самодействия» уже отличны от нуля даже при его прямолинейной конфигурации. Это легко понять, если представить этот «толстый» провод как жгут из параллельных тонких токов (если ток распределен по сечению толстого провода) или как трубу (если ток идет только по поверхности толстого провода). Такие силы стремятся сжать провод к оси. Таким эффектом объясняется сжатие плазменного шнура с током собственным магнитным полем.

Единица силы тока — ампер. Мы уже отмечали, что четвертая основная единица Международной системы единиц — ампер — определяется через магнитное взаимодействие токов. Для этого используют закон взаимодействия двух параллельных токов (7). По определению ампер — это сила неизменяющегося тока, который, проходя по двум прямым параллельным проводникам бесконечной длины и ничтожно малого поперечного сечения, расположенным в вакууме на расстоянии один от другого, создал бы между этими проводниками силу, равную на каждый метр длины.

Отсюда непосредственно получается значение магнитной постоянной которое уже использовалось выше. Из формулы (7) и определения ампера следует, что

откуда

Механическая работа в магнитном поле. Так как на проводник с током в магнитном поле действуют силы Ампера, то при движении проводника эти силы совершают определенную работу. Найдем эту работу.

Рис. 104. К вычислению работы силы Ампера при поступательном движении проводника в магнитном поле

Для простоты рассмотрим поступательное движение прямого проводника длины в однородном магнитном поле. Чтобы поддерживать в этом проводнике постоянный ток I, будем считать, что он скользит по параллельным шинам, замыкая электрическую цепь (рис. 104). Если магнитное поле с индукцией В направлено на нас, то сила Ампера действует вправо. Допустим, что проводник совершает перемещение вправо из положения 1 в положение 2. Так как перемещаемый

проводник перпендикулярен магнитному полю, то для силы Ампера справедливо выражение (3) и для работы имеем

Произведение равно заштрихованной на рис. 104 площади Произведение магнитной индукции В на равно изменению магнитного потока сквозь поверхность, ограниченную контуром с током:

Таким образом, работа силы Ампера может быть выражена через силу тока в перемещаемом проводнике и изменение магнитного потока через контур, в который включен этот проводник:

Выражая магнитный поток в веберах, а силу тока в амперах, получаем работу в джоулях.

Если магнитное поле неоднородно, то с помощью (10) можно подсчитать работу сил Ампера на тех участках, в пределах которых магнитное поле можно считать однородным, а затем суммировать работы на отдельных участках.

Отметим, что выражение (10) для работы справедливо не только для рассмотренного движения части контура, но и при любой деформации контура, сопровождающейся изменением пронизывающего его магнитного потока.

Работа силы Ампера при движении проводника с током в магнитном поле лежит в основе действия электродвигателей, в которых происходит превращение электрической энергии в механическую.

Сила Лоренца. Вернемся теперь к действию магнитного поля на ток. Так как электрический ток есть направленное движение заряженных частиц (электронов или ионов), то отсюда следует, что на движущийся заряд в магнитном поле действует сила. Получим выражение для этой силы.

На проводник длиной с током действует сила, определяемая формулой (4):

Как мы видели в предыдущем параграфе при рассмотрении магнитного поля, создаваемого движущимися зарядами, произведение может быть выражено через заряд скорость направленного движения и полное число носителей по формуле (14):

При такой замене угол а в (11) можно рассматривать как угол между вектором В и скоростью носителей, так как их направленное движение происходит вдоль провода. Таким образом, для

действующей на все носителей силы из (11) получаем

Разделив (12) на найдем силу действующую на одну частицу с зарядом движущуюся со скоростью под углом а к магнитному полю:

Эта сила перпендикулярна скорости заряда и индукции магнитного поля В, а ее модуль пропорционален синусу угла между этими векторами. Именно таким свойством обладает векторное произведение. Поэтому выражение для силы можно записать с помощью векторного произведения:

Порядок сомножителей в векторном произведении в (14) выбран так, чтобы обеспечить соответствие с правилом левой руки, определяющим направление действующей на ток силы Ампера.

Если имеется еще и электрическое поле, то полная действующая на заряд сила равна

Выражение (15) впервые было получено X. А. Лоренцем, родоначальником электронной теории строения вещества. Поэтому силу, действующую на заряд в электрическом поле, называют силой Лоренца.

Свойства силы Лоренца. Первое слагаемое в выражении (15) для силы Лоренца определяет силу, действующую на заряд со стороны электрического поля. Эта составляющая пропорциональна заряду и не зависит от его скорости. Она направлена вдоль напряженности электрического поля Е.

Второе слагаемое в (15) дает силу, действующую на заряд со стороны магнитного поля. В отличие от электрической силы, она действует только на движущийся заряд и пропорциональна его скорости. Эта сила направлена не вдоль, а поперек вектора магнитной индукции В, т. е. перпендикулярно магнитным силовым линиям.

Формула (15) имеет универсальный характер, она справедлива во всех случаях независимо от того, какими источниками создаются электрическое и магнитное поля. Она сохраняет свой вид и тогда, когда действующие на заряженную частицу электрическое и магнитное поля неоднородны в пространстве и произвольным образом изменяются со временем.

Движение заряженных частиц в электрическом и магнитном полях. При заданных полях Е и В задача о движении заряженной частицы — это обычная задача классической механики о движении под действием известных сил.

Строго говоря, движущаяся с ускорением заряженная частица излучает электромагнитные волны и испытывает с их стороны ответное воздействие. Но во многих случаях этот эффект мал и им можно полностью пренебречь. Но даже и тогда задача остается очень сложной, если заданные внешние поля неоднородны. В однородных электрическом и магнитном полях движение заряженной частицы происходит достаточно просто и может быть изучено элементарными методами.

Движение заряженной частицы в однородном электрическом поле происходит совершенно аналогично движению материальной точки в однородном поле тяжести.

Частица движется с постоянным по модулю и направлению ускорением, равным произведению удельного заряда частицы на напряженность поля Е. Траектория такого движения в общем случае представляет собой параболу. Именно так движутся электроны в пространстве между отклоняющими пластинами в вакуумной электронно-лучевой трубке осциллографа с электростатическим управлением.

Рис. 105. Поперечное движение заряженной частицы в однородном магнитном поле

Движение заряженной частицы в однородном магнитном поле под действием силы Лоренца происходит следующим образом. В плоскости, перпендикулярной индукции магнитного поля, частица равномерно обращается по окружности со скоростью (рис. 105). Радиус этой окружности пропорционален перпендикулярной магнитному полю составляющей скорости частицы а частота обращения частицы от скорости не зависит и равна произведению удельного заряда частицы на индукцию магнитного поля. Если при этом частица имеет еще и составляющую скорости вдоль магнитного поля В, то на такое вращение накладывается равномерное движение вдоль поля, так что траектория результирующего движения представляет собой винтовую линию (рис. 106). Покажем это.

Рис. 106. В однородном магнитном поле частица движется по винтовой линии

Составляющая скорости частицы вдоль магнитного поля не меняется при движении. Составляющая скорости, перпендикулярная магнитному полю, меняется только по направлению, так как действующая сила перпендикулярна скорости. Поэтому в проекции на плоскость, перпендикулярную магнитному полю, движение частицы происходит по окружности некоторого радиуса с центростремительным ускорением обусловленным силой Лоренца. Записывая

выражение для этой силы в виде и приравнивая ее в соответствии со вторым законом Ньютона произведению массы на ускорение, имеем

откуда

Частота обращения частицы как видно из (16), равна

Циклотронная частота. Независимость частоты обращения частицы в магнитном поле от ее скорости и от радиуса круговой орбиты (а тем самым и от энергии) лежит в основе принципа действия циклотрона исторически первого и наиболее простого из циклических ускорителей заряженных частиц, широко применяемого и в наши дни в самых различных областях науки и техники. От названия этого прибора происходит термин «циклотронная частота» для частоты обращения заряженной частицы в магнитном поле, даваемой формулой (17).

Отклонение заряженных частиц поперечным магнитным полем используется также в масс-спектрометрах — приборах для точных измерений масс атомов и молекул, в установках для электромагнитного разделения изотопов. В телевизионных трубках с помощью магнитного поля производится строчная и кадровая развертка электронного луча по экрану.

Интересно отметить, что при небольшом разбросе значений продольной составляющей скорости частиц движение в однородном магнитном поле обладает замечательным свойством фокусировки: выходящий из одной точки и направленный вдоль поля слегка расходящийся пучок заряженных частиц на некотором расстоянии вновь собирается в одну точку.

Рис. 107. Фокусировка пучка электронов продольным магнитным полем

Это свойство продольной фокусировки было использовано в 1922 г. Бушем для точного измерения удельного заряда электрона.

Разберем опыт Буша подробно. Рассмотрим устройство, изображенное на рис. 107: электронно-лучевая трубка без управляющих пластин помещена внутрь соленоида, создающего однородное магнитное поле, направленное вдоль оси трубки. В отсутствие магнитного

поля электроны летят прямолинейно и образуют на флуоресцирующем экране широкое светящееся пятно. Регулируя ток в соленоиде и тем самым изменяя индукцию магнитного поля, можно добиться того, что электроны соберутся на экране в яркую светящуюся точку.

Выясним причину фокусировки электронов.

Из электронной пушки электроны вылетают с приблизительно одинаковыми по модулю скоростями, но с некоторым разбросом по направлению. Скорость электрона можно определить с помощью закона сохранения энергии:

где — абсолютная величина заряда электрона, ускоряющее напряжение между катодом и ускоряющим анодом электронной пушки.

На электрон, летящий вдоль магнитного поля, сила Лоренца не действует. Поэтому электрон, вылетевший из пушки вдоль оси трубки, движется прямолинейно и попадает в центр экрана. Если же электрон вылетел под некоторым углом а к оси трубки и, следовательно, у него есть составляющая начальной скорости, перпендикулярная магнитному полю, то, как мы видели, траектория электрона представляет собой винтовую линию. Угловая скорость и, следовательно, период обращения не зависят от скорости. Поэтому электроны, вылетевшие из пушки под разными углами, совершают полный оборот за одно и то же время.

Поскольку электроны вылетают из пушки под малыми углами к оси трубки, то все они движутся вдоль оси трубки практически с одной и той же скоростью и за время одного оборота проходят вдоль оси трубки одно и то же расстояние

Это означает, что все винтовые линии, по которым движутся электроны, пересекают ось трубки практически в одной и той же точке, отстоящей на расстояние от пушки. Такая же фокусировка происходит и после совершения электронами двух, трех и т. д. оборотов, т. е. на расстояниях от пушки. Если положение одной из этих точек совпадает с плоскостью экрана, то пятно на экране сожмется в яркую точку. Расстояние от электронной пушки до экрана определяется конструкцией трубки и не изменяется во время опыта, но мы можем изменять шаг винтовой линии регулируя величину индукции магнитного поля В или ускоряющее напряжение

Подставляя скорость электронов из (18) и угловую скорость вращения из (17) в формулу (19), получаем соотношение

Если при неизменном ускоряющем напряжении мы добьемся фокусировки пучка электронов, постепенно увеличивая индукцию магнитного поля В от нуля, то формула (20) может быть использована для вычисления отношения Для этого в правую часть нужно подставить значения и В, при которых произошла фокусировка, а в качестве взять расстояние от электронной пушки до экрана трубки.

Если теперь продолжать увеличивать индукцию магнитного поля, то пятно на экране будет сначала расплываться, а затем снова сожмется в яркую точку. Ясно, что теперь электроны успевают совершить два полных оборота по винтовой линии до того, как попадают на экран. Для нахождения в формулу (20) в качестве в этом случае следует подставлять половину расстояния от пушки до экрана.

Отметим, что достигнутая этим методом погрешность измерения удельного заряда электрона составляет величину порядка десятой доли процента.

Явление фокусировки пучка электронов продольным магнитным полем используется во многих электронно-оптических приборах.

• Покажите, что при указанном на рис. 101 расположении рамки с током в магнитном поле действующий на нее вращающий момент максимален.

• Покажите, что векторная форма (5) выражения для силы Ампера соответствует правилу левой руки.

• Покажите, что параллельные токи притягиваются или отталкиваются в зависимости от того, текут они в одну или в противоположные стороны, а скрещенные токи стремятся расположиться параллельно друг другу.

• Рассмотрите вопрос о том, как действует магнитное поле, создаваемое проходящим по соленоиду током, на сам этот соленоид: стремятся ли действующие на его витки силы растянуть или сжать соленоид в продольном направлении (вдоль его в поперечном направлении?

• Как из определения единицы силы тока — ампера — установить числовое значение магнитной постоянной ?

• Входит ли в выражение (10) Для работы в магнитном поле изменение магнитного потока, создаваемого током в самом движущемся проводе? в контуре, в который он включен?

• Проверьте соответствие порядка сомножителей в векторном произведении правилу левой руки для силы, действующей на проводник с током в магнитном поле.

• Применима ли формула (15) для силы Лоренца в случае переменных во времени электрического и магнитного полей?

• Может ли сила, действующая на заряженную частицу в магнитном поле, изменить ее энергию?

• Объясните принцип фокусировки расходящегося пучка электронов в продольном магнитном поле.

• Как должна быть направлена скорость заряженной частицы в скрещенных электрическом и магнитном полях и каким должен быть ее модуль, чтобы частица двигалась прямолинейно?

• При изучении движения заряженных частиц в электрическом и магнитном полях удобно использовать метод физического подобия, изложенный в книге 1 данного курса. Примените метод подобия для получения ответа на следующий вопрос. Ионы из источника попадают в ускоряющее электрическое поле без начальной скорости и летят к детектору. Во сколько раз отличается время пролета до детектора для ионов, различающихся в два раза по заряду и в полтора раза по массе?

Поиск по сайту: