Вопрос№16 Индуктивность и емкость в цепи переменного тока

Индуктивность и емкость в цепи переменного тока. Электродинамика

Индуктивность и емкость в цепи переменного тока. Резонанс в электрической цепи.

ЦЕПЬ ПЕРЕМЕННОГО ТОКА, СОДЕРЖАЩАЯ ЕМКОСТЬ

Если в цепь постоянного, тока включить конденсатор (идеаль­ный — без потерь), то в течение очень короткого времени после включения по цепи потечет зарядный ток. После того как конден­сатор зарядится до напряжения, равного напряжению источника, кратковременный ток в цепи прекратится. Следовательно, для постоянного тока конденсатор представляет собой разрыв цепи, или, иными словами, бесконечно большое сопротивление.

Если же конденсатор включить в цепь переменного тока, то он будет заряжаться попеременно то в одном, то в другом направлении.

При этом в цепи будет проходить переменный ток. Рассмотрим это явление подробнее.

В момент включения напряжение на конденсаторе равно нулю. В течение первой четверти периода, когда напряжение сети будет возрастать (рис. 143), конденсатор будет заряжаться.

По мере накопления зарядов на обкладках конденсатора напря­жение конденсатора увеличивается. Когда напряжение сети к концу первой четверти периода достигнет максимального значения Um, напряжение конденсатора также станет равным Um, заряд конден­сатора прекращается и ток в цепи становится равным нулю. Ток в цепи конденсатора можно определить по формуле

где ∆q — количество электричества, протекающее по цепи за время ∆t.

Из электростатики известно:

где С — емкость конденсатора;

u — напряжение сети;

u_c — напряжение конденсатора. Окончательно для тока имеем

Из последнего выражения видно, что, когда ∆u/∆t максимально (положения a, в, d), i также максимально.

Когда ∆u/∆t = 0 (положения б, г на рис. 143), то i также равно нулю.

Во вторую четверть периода напряжение сети будет уменьшать­ся, и конденсатор начнет разряжаться. Ток в цепи меняет свое направление на обратное.

В следующую половину периода напряжение сети меняет свое направление и наступает перезаряд конденсатора и затем снова его разряд.

Из рис. 143 видно, что ток I в цепи с емкостью в своих изменениях опережает по фазе напряжение конденсатора на 1/4 периода, или 90°.

Сравнивая векторные диаграммы цепей с индуктивностью и емкостью, мы видим, что индуктивность и емкость на фазу тока влияют прямо противоположно.

Пользуясь высшей математикой, можно доказать, что ток в цепи с емкостью пропорционален напряжению Uc, приложенному к конденсатору, угловой частоте w и величине емкости конденсатора C:

Обозначим

Величина Хс называется емкостным сопротивле­нием, или реактивным сопротивлением ем­кости, и измеряется в омах. Выражение закона Ома для цепи переменного тока, содержащей емкость, имеет вид

Та часть напряжения сети, которая приложена к конденсатору, называется емкостным падением напряжения (или реактивной слагающей напряжения) и обозначается Uc:

Емкостное сопротивление Хс, так же как индуктивное сопро­тивление x_L, зависит от частоты переменного тока.

Но если с увеличением частоты индуктивное сопротивление увеличивается, то емкостное сопротивление, наоборот, будет умень­шаться.

Пример 6. Определить сопротивление конденсатора емкостью 5 мкф при частоте 50 гц:

при частоте 400 гц:

На рис. 144 показана кривая мгновенной мощности в цепи с емкостью. Из чертежа видно, что в первую четверть периода цепь с емкостью забирает из сети энергию, которая запасается в электрическом поле конденсатора.

Энергию, запасаемую конденсатором к моменту, когда напряже­ние на нем равно максимальному значению, можно определить по известной формуле CU²_м/2.

В следующую четверть периода конденсатор разряжается на сеть, отдавая ей ранее запасенную в нем энергию.

За вторую половину периода явление колебаний энергии пов­торяется. Таким образом, в цепи с емкостью происходит лишь обмен энергией между сетью и конденсатором без ее потерь.

Поэтому средняя за период мощность, или активная мощность, цепи с емкостью равна нулю, как и в цепи с индуктивностью.

Из графика, изображенного на рис. 144, видно, что мгновенная мощность в цепи с емкостью два раза в течение каждого периода (когда wt = 45°, 135° и т. д.) достигает максимального значения, равного

Этой величиной принято характеризовать количественно про­цесс обмена энергии между источником и электрическим полем конденсатора. Ее также называют реактивной мощностью и обозначают буквой Q.

Учитывая,, что в рассматриваемой цепи U = IХc, получим сле­дующее выражение для реактивной мощности:

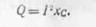
Поиск по сайту: