 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Способы записи алгоритмов. Алгоритм может иметь различные формы представления
| ← 23.4. Элементарные алгоритмические действия | 24.0. Введение → |
Алгоритм может иметь различные формы представления. Рассмотрим три наиболее распространенных из них, иллюстрируя примером алгоритма нахождения корней квадратного уравнения.
Первая и самая простая – это вербальная или словесно-формульная форма. В ней алгоритмические действия описываются словами и, при необходимости, формулами. Для выбранного примера описание алгоритма может иметь следующий вид.
Алгоритм вычисления корней квадратного уравнения ax2 + bx + c = 0. Входными данными являются коэффициенты a, b и c.
1. Сначала необходимо вычислить дискриминант уравнения D = b2 - 4ac;
2. Если дискриминант имеет неотрицательное значение, то корни уравнения - вещественные:  ;
;
3. Если дискриминант отрицательный, то корни комплексно сопряженные:  .
.
Словесно-формульная форма является естественной для человека, но, в сложных случаях, не дает четкого представления о последовательности действий и может обладать неоднозначностью их интерпретации. Она обычно используется при разработке алгоритмов как исходная.
Наиболее полной и корректной формой является запись алгоритма на специальном языке. За рубежом он называется PDL (Process Design Language), «псевдокод». Отечественный вариант этого языка был предложен академиком А.П. Ершовым в первых школьных учебниках информатики [2] и используется у многих других авторов учебников [3,4]. Это - паскалеподобный язык, обладающий всей полнотой и корректностью описания алгоритма. Алгоритм решения квадратного уравнения на нем имеет следующий вид:
алг Root2 (вещ a,b,c,x1,x2; цел key)
арг a,b,c
рез x1,x2,key
нач
вещ D,re,im
D:=b2-4ac
re:= 
im:=- 
если D>=0
то
нач
x1:=re+im
x2:=re-im
key:=0
кон
иначе
нач
x1:=re
x2:=im
key:=1
кон
все
кон
Заголовок алгоритма содержит его имя, а также описание входных (арг) и выходных (рез) данных с указанием их идентификаторов и типов. Далее аналогично описываются промежуточные данные алгоритма. Начало и конец алгоритмических действий обозначены служебными словами нач и кон. Рассматриваемый в качестве примера алгоритм очень простой и со-держит только операторы присваивания и одну структурную конструкцию – бинарное ветвление. Она оформляется служебными словами: если, то, иначе, все.
Представление алгоритма на псевдокоде допускает разные уровни абстракции и поэтому может быть использовано как при разработке алгоритма путем постепенной детализации, так и для его окончательного представления.
Третий широко распространенной формой представления алгоритмов является язык блок-схем. По корректности он занимает промежуточное положение между словесно-формульным описанием и представлением на псевдокоде. Достоинством его является визуальная наглядность графического изображения. Каждая структурная конструкция имеет стандартное графическое изображение. Некоторые из них представлены в таблице 23.1. Отдельные действия представляются в виде прямоугольников, последовательность их выполнения показываются стрелками (линиями потока).
Алгоритм решения квадратного уравнения представлен блок-схемой на рис. 23.3. Бинарное ветвление в ней представляется ромбовидной фигурой. В зависимости от значения записанного в ней логического выражения (условия) выполняется та или иная ветвь вычисления.
Блок-схемы допускают различные уровни детализации представляемых алгоритмических действий и поэтому очень удобны при разработке алгоритмов. Будучи дополнены комментариями с описаниями данных, они дают достаточно полное представлении об алгоритме.
Существуют и другие формы представления алгоритмов, имеющие более ограниченное использование, но они в данном пособии не рассматриваются. Упомянутые выше формы будут более подробно представлены ниже при описании конкретных алгоритмических структур.
Таблица 23.1. Некоторые условно-графические элементы блок-схем
| Наименование | Обозначение и относительные размеры | Функция |
| Процесс | 
| Выполнение операций или группы операций, в результате которых изменяется значение, форма представления или расположение данных |
| Решение | 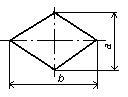
| Выбор направления выполнения алгоритма или программы в зависимости от некоторых переменных условий |
| Модификации | 
| Выполнение операций, меняющих команды или группу команд, изменяющих программу |
| Предопределенный процесс | 
| Использование ранее созданных и отдельно описанных алгоритмов или программ |
| Ввод-вывод | 
| Преобразование данных в форму, пригодную для обработки (ввод) или отображения результатов об-работки (вывод) |
| Линия потока | 
| Указание последовательности между символами |
| Пуск - останов | 
| Начало, конец, прерывание процесса обработки данных или выполнения программы |
| Комментарий | 
| Связь между элементом схемы и пояснением |
Поиск по сайту: