Базовые конструкции алгоритмов

При разработке и составлении блок-схемы того или иного алгоритма применяются следующие базовые конструкции: линейная, циклическая и ветвящаяся. В теории алгоритмов доказано, что на основе этих трех конструкций может быть построен любой алгоритм. Абсолютно все системы программирования располагают языковыми средствами для реализации основных алгоритмических конструкций.

Линейная конструкция (следование) – это последовательное выполнение операций без повторов и разветвлений (рис. 5.1).

Рис. 5.1. Линейная конструкция

Ветвящаяся конструкция (ветвление) – это выполнение операций по одному из нескольких направлений в зависимости от заданных условий (рис. 5.2).

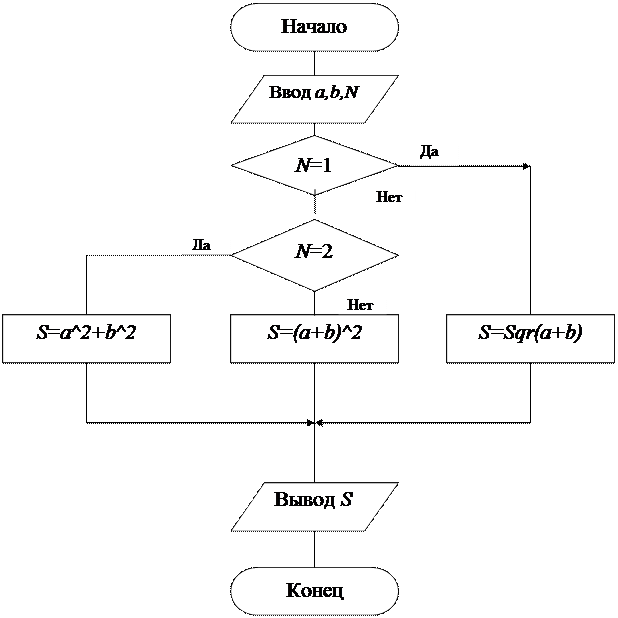
Рис. 5.2. Ветвящаяся конструкция

Циклы (конструкция повторения) используются для организации повторного выполнения какой-либо операции (инструкции) или блока операций (инструкций). Цикл состоит из двух частей: условия цикла и тела цикла. У каждого цикла есть параметр. Параметр цикла – это переменная, которая изменяется в теле цикла и задействована в условии его окончания. Для организации повторов могут применяться следующие виды циклических конструкций: цикл с предусловием, цикл с постусловием, цикл с фиксированным количеством повторов или цикл по счетчику.

Вариант 1	Вариант 2
Нет     Да	Да     Нет

Рис. 5.3. Цикл с предусловием

Вариант 1	Вариант 2
Да     Нет	Нет     Да

Рис. 5.4. Цикл с постусловием

Конструкция цикла с предусловием (рис. 5.3) в зависимости от результата выполнения условия может быть двух вариантов. В первом варианте повторение осуществляется до тех пор, пока условие имеет значение Истина (True). В другом варианте повторение осуществляется до тех пор, пока условие имеет значение Ложь (False).

Рис. 5.5. Цикл по счетчику

Вариант 1	Вариант 2

Рис. 5.6. Примеры вложенных циклов

Конструкция цикла с постусловием (рис. 5.4) в зависимости от результата выполнения условия может быть двух вариантов. В первом варианте повторение осуществляется до тех пор, пока условие имеет значение Ложь (False). В другом варианте повторение осуществляется до тех пор, пока условие имеет значение Истина (True).

В цикле по счетчику (рис. 5.5) выполнение и повторение операций происходит от начального значения параметра (счетчика) до его конечного значения с указанным шагом. Если шаг не указан, то его значение полагается равным единице.

Простые циклические конструкции могут вкладываться в другую простую циклическую конструкцию, образуя тем самым вложенный (сложный) цикл (рис. 5.6). При этом необходимо придерживаться следующих правил:

· имена параметров всех простых циклов не должны повторяться;

· нельзя войти во внутренний (вложенный) цикл, минуя внешний;

· простые циклы в сложном цикле не должны пересекаться, то есть внешний цикл должен заканчиваться после внутреннего и инструкции тела внешнего цикла не должны быть
в теле внутреннего цикла.

5.1.3. Контрольные вопросы

1) Как называется конечная последовательность точно определенных действий?

2) Перечислите основные свойства алгоритмов.

3) В каком свойстве выражается точность и однозначность каждого предписания алгоритма?

4) Что характеризует свойство алгоритма результативность?

5) Как называется возможность расчленения задачи на ряд элементарных шагов?

6) Перечислите типовые структуры (модели) алгоритмов.

7) Как называется алгоритмическая конструкция, в соответствии с которой инструкции выполняются в порядке естественного их следования?

8) Как называется алгоритм, содержащий два или более разветвлений вычислительного процесса?

9) Каково название алгоритма, обеспечивающего неоднократное выполнение последовательности инструкций?

10) Назовите способ, не применяемый для описания алгоритмов.

11) В виде какой фигуры изображается оператор вывода на блок-схеме?

12) В виде какой фигуры изображается оператор ветвления на блок-схеме?

13) Что можно вписать в блок-схеме внутри графической фигуры, похожей на овал?

14) Как называется и для чего в блок-схеме используется графическая фигура ромб?

15) Определите начальное значение x при выполнении алгоритма
(y = x + 6: x = y: y = x + y), значение переменной y = 14.

16) Определите начальное значение x при выполнении алгоритма
(y = x + 2: x =2 × y: y = x + y), значение переменной y = 12.

17) Какие значения получат c и d в результате выполнения алгоритма (a = 8: b = 3: если a < b, то c = b − a, иначе с = 2 × (a − b): d = 0: пока c > a выполнить действия:d = d + 1, c = c −1)?

18) Определите количество повторений цикла в фрагменте алгоритма (a = 3: b = 7: пока a / b <= b / 3: a = a + 2: b = b + 3).

19) Какие значения получат элементы массива в результате выполнения алгоритма (i = 2: N = 8: пока i <= N: A(i) = i × i: i = i + 2)?

20) Какие значения получат элементы массива в результате выполнения алгоритма (i = 1: N = 4: пока i <= N: A(i) =i × 2 + 2: i= i+ 1)?

21) Что представляет собой R, полученное в результате выполнения алгоритма (R = 1: N = 10: i = 2: пока i <= N: если x(i) < 0
тогда R = R × x(i): i= i + 2: вывод R), по отношению к элементам заданного массива: x(1), x(2),..., x(n)?

22) Что представляет собой K, полученное в результате выполнения алгоритма (K = 0: N = 10: i = 1: пока i <= N: если x(i) = 0 тогда K = K + 1: i = i + 1: вывод K), по отношению к элементам заданного массива: x(1), x(2),..., x(n)?

23) Что представляет собой S, полученное в результате выполнения алгоритма (S = 0: N = 10: i = 1: пока i <= N: если x(i) > 0 тогда S = S + x(i): i = i + 1: вывод S), по отношению к элементам заданного массива: x(1), x(2),..., x(n)?

24) Что необходимо изменить, чтобы бесконечный цикл, содержащийся во фрагменте алгоритма (x = 10: пока x >= 10:
x = x + 1), стал конечным?

25) Какое значение будет выведено в результате выполнения алгоритма (N = 0: y = 0: пока N < 10: y = y + N: N = N + 1: вывод y)?

Поиск по сайту: