Алгоритм получения дополнительного k-разрядного кода отрицательного числа

Определение 7. В p-ичной системе счисления любое неотрицательное вещественное число можно записать в виде

,

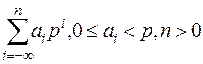
где p > 1 – основание позиционной системы счисления,

a_i – цифры числа a в p-ичной системе счисления.

Отрицательные числа в p - ичных системах счисления представляются с помощью знака минус перед выражением для модуля отрицательного числа.

Определение 8. Представление числа в привычной для человека форме «знак-величина», при которой старший разряд ячейки отводится под знак, остальные k-1 разрядов – под цифры числа, называется прямым кодом.

Например, прямые коды двоичных чисел 11001₂ и -11001₂ для восьмиразрядной ячейки соответственно равны 00011001
и 10011001.

Положительные целые числа представляются в компьютере
с помощью прямого кода.

Отрицательные целые числа представляются в компьютере
с помощью дополнительного кода.

Определение 9. k-разрядный дополнительный код отрицательного числа m – это запись в k разрядах положительного числа 2 ^k - |m|, где |m| – модуль отрицательного числа m, |m| <= 2 ^{k -1}.

Алгоритм получения этого кода выглядит следующим образом:

1) модуль отрицательного числа представить прямым кодом в k двоичных разрядах;

2) значения всех разрядов инвертировать (все нули заменить единицами, а единицы – нулями), получив, таким образом,
k- разрядный обратный код исходного числа;

3) к полученному обратному коду, трактуемому как
k- разрядное неотрицательное двоичное число, прибавить единицу.

Пример: Найдем дополнительный код числа -52.

Для восьмиразрядной ячейки:

0011 0100 – прямой код числа |-52| = 52;

1100 1011 – обратный код числа 52;

1100 1100 – дополнительный код числа -52.

Для шестнадцатиразрядной ячейки:

0000 0000 0011 0100 – прямой код числа |-52| = 52;

1111 1111 1100 1011 – обратный код числа 52;

1111 1111 1100 1100 – дополнительный код числа -52.

Описанный выше алгоритм получения дополнительного кода для отрицательного числа знаковую единицу в левом разряде образует автоматически при |m| <= 2 ^{k - 1}.

Если же 2 ^{k -1} < |m| < 2 ^k, то попытка реализации данного алгоритма приведет к тому, что в левом разряде будет находиться цифра 0, соответствующая компьютерному представлению положительных чисел, что неверно.

Восстановить модуль отрицательного исходного десятичного числа по его дополнительному коду можно двумя способами.

Способ 1 (обратная цепочка преобразований):

1) вычесть единицу из дополнительного кода;

2) инвертировать полученный код;

3) перевести полученное двоичное представление числа в десятичное.

Способ 2: по приведенному выше алгоритму построить дополнительный код для имеющегося дополнительного кода искомого числа и представить результат в десятичной системе счисления.

Пример получения десятичного значения числа по его дополнительному коду 10010111₂.

Способ 1:

1) из дополнительного кода вычитаем единицу

10010111 - 1 = 10010110 (получили обратный код);

2) инвертируем полученный обратный код 01101001

(получили модуль отрицательного числа);

3) переводим полученное двоичное значение в десятичную систему счисления:

01101001₂ = 2⁶ + 2⁵ + 2³ + 1 = 64 + 32 + 8 + 1 = 105.

Способ 2:

1) инвертируем имеющийся дополнительный код: 01101000;

2) прибавляем единицу: 01101000 + 1 = 01101001 (получили модуль отрицательного числа);

3) переводим полученное двоичное значение в десятичную систему счисления:

01101001₂ = 2⁶ + 2⁵ + 2³ + 1 = 64 + 32 + 8 + 1 = 105.

В таблице, расположенной ниже, приведены значения границ диапазонов для знаковых представлений в ячейках с различной разрядностью.

Поиск по сайту: