Расчет среднего и дисперсии элементов в массивах

Среднее значение Xmean одномерного массива (выборки), состоящего из n элементов, и его дисперсия D рассчитываются по известным формулам:

.

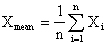
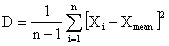Корень квадратный из дисперсии называется среднеквадратичным отклонением S.

Блок-схема алгоритма приведена на рис. 28.12. Сначала считается среднее значение, а затем – дисперсия. Суммы накапливаются в циклах по переменной i – индексу суммирования. Циклы имеют одинаковые параметры, но объединять их, на первый взгляд, нельзя, так как второй цикл использует результат, появляющийся при завершении первого. Но если преобразовать формулу для дисперсии, раскрывая квадрат разности, то можно получить:

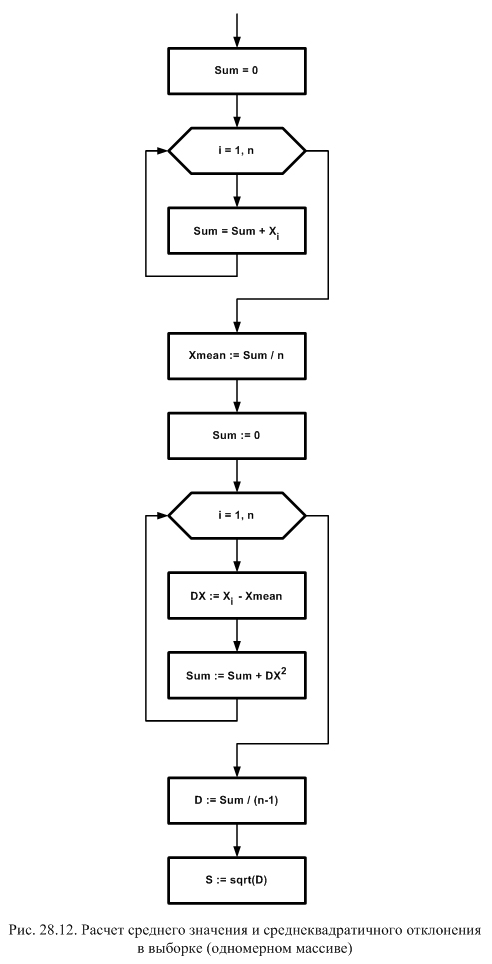
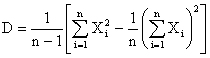
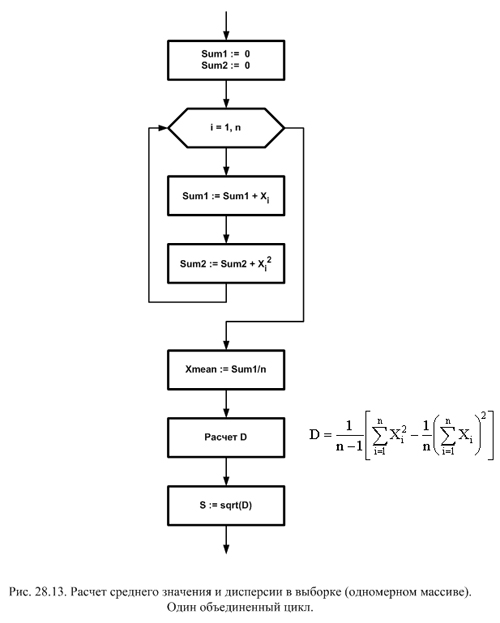
При этом появляется две суммы – сумма элементов массива и сумма их квадратов, которые накапливаются в одном цикле. Блок-схема этого варианта алгоритма приведена на рис. 28.13.

Поиск по сайту: