Возведение в степень по модулю

Определение x ^y (mod n) при x, y > 0 совпадает с определением обычной степени целого числа (т.е = x x x … x (y раз) (mod n)).

Введем операцию целочисленного деления на 2 (y ÷ 2):

y÷ 2 =		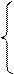y /2, если y – четно
(y –1)/2, если y – нечетно

Тогда:

x y=		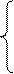(x 2) (y ÷ 2), если y – четно
x (x 2) (y ÷ 2), если y – нечетно

Алгоритм возведения целого числа в степень по модулю

ВХОД: x, y, n: целые числа x> 0, y≥ 0 n > 1

ВЫХОД: x^{, y} (mod n).

Е (x, y, n)

1. if y = 0 return (1);

2. if y (mod 2) = 0 return (E (x²(mod n)), (y ÷ 2), n);

3. return (x ∙E (x²(mod n)), (y ÷ 2), n) (mod n).

Операция return (значение) возвращает процесс вычисления в точку вызова функции Е (т.е. если выполнен шаг 2, то шаг 3 не будет реализован).

Пример 1 Вычислить 2²¹(mod 23).

2²¹(mod 23) = Е (2, 21, 23) = 2∙ Е (4, 10, 23) = 2∙ Е (16, 5, 23) = 2∙ 16∙Е (16², 2, 23) =

= (2∙ 16)(mod 23) ∙Е (16²(mod 23), 2, 23) = 9∙Е (3, 2, 23) = 9∙Е (9, 1, 23) = 81∙Е (9, 0, 23) =

=81 (mod 23) = 12.

Ответ: 2²¹(mod 23) ≡ 12.

Пример 2 Вычислить 3²¹(mod 23).

3²¹(mod 23) = Е (3, 21, 23) = 3∙ Е (9, 10, 23) = 3∙ Е (81, 5, 23) = 3∙ 12∙Е (12², 2, 23) =

= (3∙ 12)(mod 23) ∙Е (12²(mod 23), 2, 23) = 13∙Е (6, 2, 23) = 13∙Е (36(mod 23), 1, 23) =

= 13∙Е (13, 1, 23) = 13∙13∙Е (13, 0, 23) = 169 (mod 23) = 8.

Ответ: 3²¹(mod 23) ≡ 8.

Пример 3 Вычислить 11²¹(mod 23).

11²¹(mod 23) = Е (11, 21, 23) = 11∙ Е (121(mod 23),10,23) = 11∙ Е (6,10,23) = 11∙ Е (36,5,23) =

= 11∙ Е (13, 5, 23) = 11∙13∙Е (169, 2, 23) = 5∙Е (8, 2, 23) = 5∙Е (64, 1, 23) = 5∙Е (18, 1, 23) =

= 5∙18∙Е (18, 0, 23) = 90 (mod 23) = 21. Ответ: 11²¹(mod 23) ≡ 21.

Поиск по сайту: