Глава VII. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В СИСТЕМАХ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ (ОБЩАЯ ПОСТАНОВКА ЗАДАЧИ)

Вынужденные колебания наблюдаются в системах при внешнем силовом воздействии. Это воздействие должно иметь ту же физическую природу, что и система, на которую оно действует. Обычно предполагается, что внешний источник действует бесконечно долго, так что собственные колебания к моменту наблюдения затухли и в системе сохраняются только вынужденные колебания.

Если воздействие прекращается, вынужденные колебания исчезают. Получим динамическое уравнение системы при силовом воздействии. В качестве примера рассмотрим последовательный колебательный контур под действием источника ЭДС (Рис.45).

Применяя второй закон Кирхгофа, получим уравнение для заряда:

. (7.1)

Пусть в качестве искомой переменной будет напряжение на емкости

. (7.2)

Тогда, вводя стандартные обозначения

, (7.3)

получим уравнение в стандартной форме

. (7.4)

Если система нелинейная, уравнение в общем случае имеет вид:

. (7.5)

С математической точки зрения анализ вынужденных колебаний означает отыскание решения неоднородного дифференциального уравнения.

Решение нелинейного уравнения (7.5) в общем виде неизвестно, поэтому обычно рассматривают частные случаи. (В следующих лекциях рассмотрим задачу Дуффинга).

Для анализа линейных систем (7.1) существует ряд мощных методов: метод вариаций постоянной Лагранжа, метод Лапласа, метод Фурье и другие. Применение того или иного метода определяется в основном видом функции

Из теории обыкновенных дифференциальных уравнений известно, что общее решение неоднородного линейного уравнения (7.1) можно представить в виде:

, (7.6)

где - решение однородного уравнения (2.7); представляет собственные колебания системы, которые подробно изучались выше. - частные решения неоднородного уравнения, которое описывает вынужденные колебания. Найти и проанализировать его – наша задача. Важно помнить, что четкое разделение собственных и вынужденных колебаний возможно только в линейных системах. По существу – это следствие выполнения принципа суперпозиции в линейных системах.

Напомним содержание этого принципа применительно к уравнению (7.1).

Если - частное решение при , а 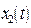- частное решение при , то при

, (7.7)

где - постоянные коэффициенты, частным решением уравнения будет

. (7.8)

Легко проверить, что выражение (7.6) является частным случаем (7.8), соответствующим .

Для нелинейного уравнения (7.5) принцип суперпозиции не выполняется, поэтому выделение вынужденных колебаний в чистом виде невозможно.

Из всего многообразия внешних воздействий, особое значение имеет гармоническое воздействие. Из теории рядов Фурье и интеграла Фурье известно, что при определенных ограничениях (которые всегда выполняются на практике) функция времени может быть представлена в виде суммы гармонических колебаний. Кроме того, гармонические колебания относительно просто генерировать. Таким образом, гармоническая функция играет роль фундаментальной функции.

Поэтому исследование вынужденных колебаний в любой системе начинается обычно со случая гармонического воздействия.

Поиск по сайту: