Глава VIII. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В ЛИНЕЙНОЙ СИСТЕМЕ ПРИ ГАРМОНИЧЕСКОМ ВОЗДЕЙСТВИИ

Уравнение системы (7.1) для этого случая примет вид:

, (8.1)

где - частота внешнего источника, - амплитуда и начальная фаза соответственно.

Частное решение уравнения (8.1) найдем методом комплексных амплитуд. Этот метод прост и экономичен, но применим только для линейных систем при гармоническом воздействии. Алгоритм метода проиллюстрирован ниже.

Вместо уравнения (8.1) интегрируется уравнение:

, (8.2)

где, по определению,

, (8.3)

комплексная амплитуда внешней силы. Физическая амплитуда равна модулю комплексной амплитуды

, (8.4)

а начальная фаза – аргументу

. (8.5)

Правая часть уравнения (8.2) по формуле Эйлера:

, (8.6)

т.е. внешняя сила представляет суперпозицию двух колебаний:

, (8.7)

где

, (8.8)

. (8.9)

Сравнивая (7.8) и (8.7), видим . По принципу суперпозиции частное решение (8.2) имеет вид:

, (8.10)

где

, (8.11)

частное решение при косинусоидальном воздействии (8.8):

, (8.12)

частное решение при синусоидальном воздействии (8.9). Частное решение ищем в форме, аналогичной (8.7),

, (8.13)

где - комплексная амплитуда вынужденных колебаний. Аналогично (8.3),(8.4),(8.5)

, (8.14)

(8.15)

- действительная амплитуда вынужденных колебаний,

(8.15)

- начальная фаза.

Из (8.11)

. (8.16)

Из (8.12)

. (8.17)

Таким образом, вынужденные колебания (8.16) для системы (8.1) ищутся в виде косинусоидального колебания с частотой внешнего воздействия. При использовании комплексных амплитуд не важно, действует ли косинусоидальная или синусоидальная сила, имеет значение тот факт, что колебание гармоническое с частотой .

Информация о том, что колебание гармоническое частоты содержится в показательном множителе .

Теперь покажем, как найти неизвестную . Подставим (8.13) в уравнение (8.2). Легко видеть, что производная по времени соответствует умножению комплексной амплитуды на

. (8.18)

После подстановки

. (8.19)

Сокращая на общий множитель (что возможно лишь в линейных уравнениях!), получаем алгебраическое уравнение относительно неизвестной комплексной амплитуды . Суть метода комплексных амплитуд в том и состоит, что решение дифференциального уравнения (8.1) путем введения комплексных амплитуд сводят к более простой задаче: к решению алгебраического уравнения (8.19).

Решая (8.18)относительно комплексной амплитуды:

. (8.20)

Реальная амплитуда (8.15);

. (8.21)

Чтобы найти начальную фазу 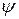, перепишем (8.21) в виде;

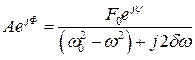. (8.22)

Перенесем из правой части в левую

. (8.23)

Тогда

. (8.24)

Итак, вынужденные колебания в линейной системе при косинусоидальном колебание (8.16), где амплитуда и начальная фаза определяются в выражением (8.21) и (8.24). Аналогичный результат будет и при синусоидальном воздействии.

Обобщая эти результаты, можно сделать общий вывод: при воздействии на линейную систему внешней гармонической силы с частотой в системе возбуждаются гармонические колебания той же частоты , но с амплитудой начальной фазой, определяемыми не только параметрами внешней силы, но и параметрами линейной системы.

Из (8.21) видно, что амплитуда вынужденных колебаний линейно зависит от амплитуды внешнего воздействия. Отсюда отношение;

, (8.25)

оказывается только функцией частоты и параметров самой системы. В теории цепей как функция частоты, известно как амплитудно–частотная характеристика (АХЧ). Из (8.24) следует, что сдвиг фаз между внешней силой и вынужденными колебаниями определяется частотой и параметрами линейной системы. Зависимость сдвига фаз от частоты известна как фазово–частотная характеристика (ФЧХ).

Частотные характеристики (АЧХ и ФЧХ) имеют смысл для систем любой физической природы: электрической, механической и т.д. Вычисление (или измерение) частотных характеристик и их анализ – вот цель частотных методов исследования линейных систем.

Рассмотрим подробней частотные зависимости для частных, но важных случаев.

Вынужденные колебания в гармоническом осцилляторе при гармоническом воздействии.

Динамическое уравнение системы

. (8.26)

Оно представляет частный случай уравнения (8.1), если . Выбор 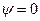не принципиален, так как начальная фаза определяется началом отсчёта во времени. Условие существенно, так как означает отсутствие потерь. Частное решение (8.26) ищем в виде (см. (8.16));

. (8.27)

Комплексная амплитуда (8.20):

. (8.28)

Комплексная амплитуда является вещественной, поэтому вынужденное колебание (8.27)примет вид:

. (8.29)

Амплитудно – частотная зависимость:

. (8.30)

Фазо–частотная зависимость с учётом вещественной

. (8.31)

Графики частотных зависимостей приведены на рисунке 46.

Видно, что амплитуда быстро растёт по мере приближения частоты внешней силы к собственной частоте осциллятора, а при точном совпадении амплитуда остановится бесконечной.

Явлений резкого возрастания амплитуды вынужденных колебаний в системе на некоторой частоте внешнего воздействия называется резонансом.

Частота внешнего гармонического сигнала, при которой амплитуда максимальна, называется резонансной. Для гармонического осциллятора резонансная частота равна частоте собственных колебаний. Что касается начальной фазы, то на резонансной частоте происходит скачок фазы на .

В реальном устройстве не наблюдается ни бесконечная амплитуда, ни скачок фазы. Расхождения теорий и опытных данных есть результат неточности модели. Естественное уточнение модели - это учёт потерь.

Поиск по сайту: