 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Глава V.СВОБОДНЫЕ КОЛЕБАНИЯ В СИСТЕМЕ С КУЛОНОВСКИМ ТРЕНИЕМ
 В качестве объекта исследования возьмем нелинейную диссипативную систему, в которой потери обусловлены кулоновским трением. Сила трения есть функция скорости
В качестве объекта исследования возьмем нелинейную диссипативную систему, в которой потери обусловлены кулоновским трением. Сила трения есть функция скорости  . При вязком трении сила трения пропорциональна скорости. Сила кулоновского трения слабо зависит от величины скорости, а лишь зависит от знака скорости. График этой зависимости представлен на рис.34 пунктирной линией. Обычно зависимость
. При вязком трении сила трения пропорциональна скорости. Сила кулоновского трения слабо зависит от величины скорости, а лишь зависит от знака скорости. График этой зависимости представлен на рис.34 пунктирной линией. Обычно зависимость  аппроксимируется ломаной.
аппроксимируется ломаной.
Аналитическая запись имеет вид:
 , (5.1)
, (5.1)
или вводя обозначение сигнатуры
 , (5.2)
, (5.2)
 , (5.3)
, (5.3)
 Часто кулоновское трение называется сухим, так как оно встречается в механических системах с трущимися поверхностями. В электрических системах его аналога не существует.
Часто кулоновское трение называется сухим, так как оно встречается в механических системах с трущимися поверхностями. В электрических системах его аналога не существует.
Возьмем систему с кулоновским трением, изображенную на рис.35.
Между грузом m и платформой существует сухое трение. Уравнение такой системы имеет вид:
 , (5.4)
, (5.4)
где ( -упругая сила).
-упругая сила).
После преобразования, с учетом (5.3)
 . (5.5)
. (5.5)
Это уравнение справедливо только при  , когда сила упругости больше силы трения. Если
, когда сила упругости больше силы трения. Если  , движение прекращается.
, движение прекращается.
Если отклонение  находится в интервале
находится в интервале  , движение системы отсутствует. Интервал
, движение системы отсутствует. Интервал  называется областью застоя.
называется областью застоя.
Преобразуем уравнения, вводя собственную частоту механической системы без трения
 . (5.6)
. (5.6)
Тогда
 , (5.7)
, (5.7)
 . (5.8)
. (5.8)
Уравнение системы с кулоновским трением является нелинейным. Скачкообразную функцию  невозможно заменить прямой ни при каких
невозможно заменить прямой ни при каких 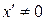 , следовательно, система с кулоновским трением не может описываться линейным уравнением в принципе.
, следовательно, система с кулоновским трением не может описываться линейным уравнением в принципе.
Решение нелинейных уравнений представляет трудную задачу, так нет регулярных методов решения. Но с некоторыми методами, которыми пользуются на практике, мы и познакомимся в теории колебаний. Задачу о движении системы с кулоновским трением мы решим методом сшивания. Его также называют методом припасовывания, или методом поэтапного рассмотрения.
В чем суть метода? Движение нелинейной системы разбивают на этапы, каждый из которых описывается известным уравнением. Уравнения интегрируются, а затем решения сшиваются, т.е. конечные значения одного этапа служат начальным условием для решения следующего этапа.
Идея этого метода проста, но реализовать его трудно, так как нет критериев, как разбивать движение на этапы.
В случае системы с кулоновским трением эти этапы очевидны:
1 этап – скорость  положительная,
положительная,
2 этап – скорость  отрицательная.
отрицательная.
Соответственно уравнения системы:
1.  при
при  (5.9)
(5.9)
2.  при
при  (5.10)
(5.10)
Легко видеть, что оба уравнения являются линейными. Если ввести переменные
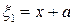 , (5.11)
, (5.11)
 , (5.12)
, (5.12)
то уравнения примут вид:
 при
при  , (5.13)
, (5.13)
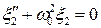 при
при  . (5.14)
. (5.14)
По форме эти уравнения гармонического осциллятора, решение которых нам хорошо известно.
С учетом (5.11) и (5.12) можно записать решения на соответствующих этапах:
I.  , (5.15)
, (5.15)
если  ; (5.16)
; (5.16)
II. 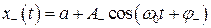 , (5.17)
, (5.17)
если  . (5.18)
. (5.18)
Неизвестные постоянные 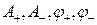 найдем из начальных условий и используя сшивание решений:
найдем из начальных условий и используя сшивание решений:
 . (5.19)
. (5.19)
Пусть в начальный момент 
 ,
,
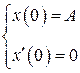 . (5.20)
. (5.20)
I этап:
При  необходимо взять решение (5.17), так как начальные условия соответствуют максимуму
необходимо взять решение (5.17), так как начальные условия соответствуют максимуму  при
при  и, следовательно, при
и, следовательно, при  функция
функция  убывает
убывает  .
.
Найдем  . При
. При 
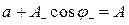 , (5.21)
, (5.21)
 . (5.22)
. (5.22)
Из второго уравнения следует, что-либо 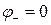 , либо
, либо  . Поскольку по определению амплитуды
. Поскольку по определению амплитуды  положительны и
положительны и  , то должно выполняться
, то должно выполняться 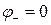 и
и
 . (5.23)
. (5.23)
Окончательно на первом этапе;
 , (5.24)
, (5.24)
 . (5.25)
. (5.25)
Из условия  получаем, что первый этап длиться во времени полпериода
получаем, что первый этап длиться во времени полпериода  .
.
При 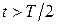 решение (5.24) использовать нельзя, так как
решение (5.24) использовать нельзя, так как  . При
. При  начинается 2 этап. Колебание системы можно описывать выражением (5.15)
начинается 2 этап. Колебание системы можно описывать выражением (5.15)
 . (5.26)
. (5.26)
Найдем постоянные 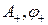 при сшивании решений на 1 и 2 этапах. При
при сшивании решений на 1 и 2 этапах. При  скорость равна 0:
скорость равна 0:
 (5.27)
(5.27)
и колебание непрерывно, т.е.
 . (5.28)
. (5.28)
Отсюда
 , (5.29)
, (5.29)
 . (5.30)
. (5.30)
Учитывая, что  , амплитуда
, амплитуда  положительна, получим, что
положительна, получим, что
 , (5.31)
, (5.31)
 . (5.32)
. (5.32)
По времени второй этап длиться в интервале 
 . (5.33)
. (5.33)
Для  начинается 3 этап. Используя условие сшивания
начинается 3 этап. Используя условие сшивания
 , (5.34)
, (5.34)
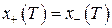 . (5.35)
. (5.35)
легко проверить, что при 
 (5.36)
(5.36)
и т. п.
По индукции можно записать общий результат: на (n+1) этапе при  , где n=0,1,2…
, где n=0,1,2…
 . (5.37)
. (5.37)
Колебания будут продолжаться до тех пор, пока  , или что эквивалентно,
, или что эквивалентно,
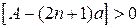 . (5.38)
. (5.38)
Очевидно, что наступит такой момент (число n), когда это неравенство нарушится. Движение в системе прекратится.
Все решения поэтапно можно изобразить в виде приведенного ниже графика (Рис.36). Видно, что колебания затухают. Если силы трения оказываются больше сил упругости, движение прекращается. Число колебаний в системе с сухим трением конечно; оно тем больше, чем больше начальная амплитуда и меньше величина трения. Условная частота равна собственной частоте системы без трения.

Поиск по сайту: