Глава III. МЕТОД ФАЗОВОЙ ПЛОСКОСТИ

Понятие фазовой плоскости заимствовано теорией колебаний из механики.. Если механическая система состоит из тел, или в общем случае имеет степеней свободы, то состояние системы в момент t, или что то же самое, фаза системы описывается совокупностью координат и импульсов . Пространство координат и импульсов называется фазовым пространством. Если система описывается одной координатой и одним импульсом (система с одной степенью свободы), то пространство вырождается в плоскость, которая и называется фазовой плоскостью.

В теории колебаний принято называть фазовой плоскостью плоскость координаты и скорости .Такое определение не меняет смысла фазовой плоскости, так как импульс и скорость связаны линейно . В электрических системах роль координаты может играть заряд q, тогда скорость есть ни что иное, как ток . Если цепь содержит емкость, то заряд и напряжение на емкости линейно связаны;

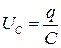. (3.1)

Таким образом, плоскость- напряжение на емкости, ток через емкость- также может рассматриваться как фазовая плоскость электрической системы. Аналогичный вывод можно сделать относительно напряжения на индуктивности 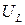и тока через индуктивность , так как

. (3.2)

Обобщая это, можно утверждать, что фазовая плоскость для электрических цепей – это плоскость .

Состояние системы в фиксированный момент времени описывается ее координатой и скоростью . На фазовой плоскости состояние соответствует точке с координатами .Эта точка называется изображающей точкой. (Рис.11).

Стечением времени координата и скоростью изменяются, соответственно изображающая точка движется по фазовой плоскости. След движения изображающей точки называется фазовой траекторией. Направление движения изображающей точки указывается стрелкой.

Совокупность фазовых траекторий, соответствующих различным начальным условиям, называется фазовым портретом системы

Построение фазового портрета является необходимым этапом при анализе системы методом фазовой плоскости.

Метод фазовой плоскости обладает и достоинствами, и недостатками. Перечислим достоинства метода:

1. Наглядность, так как результаты обычно представлены в графической форме, в виде фазового портрета;

2. Универсальность в том смысле, что метод применим как к линейным, так и к нелинейным системам. Очень важно, что нелинейная система может иметь любую нелинейность.

3. Возможность анализа системы в широком диапазоне начальных условий.

Укажем на те недостатки, которые ограничивают применение метода фазовой плоскости

1. Используется только при анализе систем с одной степенью свободы. При исследовании систем с двумя и более степенями свободы фазовое пространство становится многомерным, представление результатов в графической форме- невозможным, наглядность теряется.

2. Метод фазовой плоскости применим только к автономным системам, т.е. системам без внешнего воздействия.

3. Метод является качественным. По фазовому портрету можно судить о характере движения (колебательное, лимитационное), но точное поведение системы во времени остается неизвестным.

Каковы же этапы исследования системы методом фазовой плоскости?

1. Уравнение нелинейной системы представляется в стандартной форме – в виде двух уравнений первого порядка

. (3.3)

Если есть уравнение второго порядка, то можно перейти к уравнениям первого порядка. Например, возьмем уравнение математического маятника

. (3.4)

Обозначим и с учетом уравнения (3.3) получим

. (3.5)

Сравнивая (3.3) и (3.5), видим, что

. (3.6)

2. Исключаем время. Для этого формально делим левые и правые части уравнений (3.3) и, используя правила математического анализа

. (3.7)

Окончательно получаем уравнение фазовых траекторий

. (3.8)

Мы видим, что порядок уравнения понизился, Было уравнение второго порядка по времени (3.4), а получилось уравнение первого порядка, но относительно координаты.

Если же система неавтономна, то в правой части уравнения (3.1) входит явная функция времени, например

) (3.9)

и порядок уравнения (3.4) понизить не удается, так как время не исключается. Именно по этой причине фазовая плоскость используется для исследования только автономных систем.

3. Интегрируем уравнение (3.8). Уравнение в общем виде нелинейное, поэтому точное решение 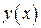удается получить только для конкретных функций и 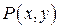. В том случае, если точного решения уравнения (3.8) найти не удается, то используют приближенные методы нахождения решения. Один из таких приближенных методов известен как метод изоклин. графического интегрирования- метод изоклин. Рассмотрим его.

Хорошо известен геометрический смысл производной Это тангенс угла наклона касательной к кривой 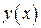. Таким образом, по уравнению (3.8), всегда можно найти тангенс угла наклона касательной к интегральной кривой, проходящей через заданную точку . В методе изоклин фиксируют угол наклона касательной (Рис.12)

. (3.9)

Из (3.8) получаем уравнение изоклины в неявной форме

. (3.10)

Изоклина представляет собой геометрическое место точек, в которых касательные к интегральным кривым имеют одинаковый угол наклона.

Уравнение для изоклины (3.10) является алгебраическим и с математической точки зрения более простым, чем дифференциальной (3.8). В простейших случаях удается найти выражение для изоклины в явной форме;

. (3.11)

Если обратиться к уравнению (3.9), тот оно имеет решение . Представляя его в (3.10), необходимо проверить не обратится ли оно в тождество при некоторых . Если это имеет место, то соответствующая изоклина является и интегральной кривой уравнения (3.8). Задавая разные углы наклона 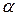, будем получать соответствующие изоклины. Черточки на изоклинах указывают направление касательных. Имея график семейства изоклин, можно построить приближенную интегральную кривую, т.е. получить приближенное решение уравнения (3.8) в графической форме.

Правило построения следующее (рис.13): из начальной точки 1 проводят в сторону следующей изоклины две прямые: одна совпадает с касательной первой изоклины, другая- с касательной следующей изоклины. Отрезок между двумя пересечениями с изоклиной делятся пополам, и находим точку 2. Соединяя точки 1 и 2 отрезком прямой, получаем приближенный график участка интегральной кривой.

Теперь считая точку 2 начальной, повторяем аналогичное построение и получаем точку 3 и т.д. Очевидно, чем больше изоклин, тем ближе ломаная к истиной интегральной кривой. Метод изоклин в принципе позволяет получить интегральную кривую любой заданной точностью.

Для того чтобы интегральная кривая уравнения (3.4) стала фазовой траекторией, надо стрелкой указать направление движения изображающей точки со временем. Для этого необходимо привлекать исходные динамические уравнения (3.3)

4. Обязательным этапом исследования системы уравнений (3.8) является отыскание особых точек на фазовой плоскости. Особые точки уравнения (3.8) соответствуют таким значениям , при которых числитель и знаменатель одновременно обращаются в нуль;

, (3.12)

При этом правая часть уравнения (3.8) становится неопределенной и нарушаются условия теоремы Коши о единственности решения уравнения. Через особую точку может проходить несколько интегральных кривых или не проходить не одной.

Чтобы уяснить физический смысл особых точек, обратимся к динамическим уравнениям.(3.3) Условия(3.12) эквивалентно

, (3.13)

координата и скорость системы не зависит от времени, что означает, что система находится в стационарном состоянии, в частности состоянии равновесия. Определения равновесных состояний очень важно на практике. Отсюда особую роль, которую играют особые точки.

Особые точки классифицируются, причем тип особой точки определяется характером фазовой траектории, вблизи особой точки. Если же говорить о движении исследуемой системы, то тип особой точки несет информацию о характере движения вблизи состояния равновесия.

Рассмотрим подробно на примерах анализа линейных систем типы особых точек, построим фазовые портреты и, сравнивая их с точечными решениями динамических уравнений, покажем, как по фазовому портрету можно судить о движении системы во времени.

Поиск по сайту: