Особая точка типа фокус

Рассмотрим особую точку типа фокус на примере линейной системы с малым затуханием. Динамическое уравнение для такой системы имеет вид

, (3.22)

а условия малости затухания записывается в виде .

Перейдем к уравнениям в стандартной форме

. (3.23)

Исключаем время и получим уравнение фазовых траекторий

. (3.16)

Особые точки будут при условии, что

. (3.17)

Особая точка соответствует началу координат: и .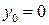

С физической точки зрения особая точка – это состояние равновесия.

Проинтегрируем уравнения (3.16), чтобы узнать, как ведут себя интегральные кривые вблизи особой точки. Из теории обыкновенных дифференциальных уравнений известны методы интегрирования подобных уравнений, однако это связано с громоздкими вычислениями (желающим это предлагается проделать самостоятельно). Мы же используем для интегрирования метод изоклин. Тем более что, с его помощью мы сразу получим фазовую траекторию.

Зафиксируем угол наклона касательно интегральной кривой 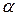.Тогда

. (3.18)

Из (3.12) получим алгебраическое уравнение изоклины в неявной форме;

. (3.19)

Проверим, не является ли изоклина интегральной кривой. Подставим в уравнение изоклины и получим

. (3.20)

После преобразований получаем уравнение относительно k:

. (3.21)

Оно совпадает с характеристическим уравнением, корни которого комплексные. Значит, изоклина не является интегральной кривой.

Найдем уравнение изоклины из (3.19) в явной форме;

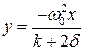. (3.22)

Как видно, мы получили уравнение прямой. Изоклины представляют собой прямые, которые проходят через начало координат и имеют разные углы наклона. Составим небольшую таблицу (Таблица 1), полагая разными значениями углов касательных к интегральным кривым.

Таблица 1

Углы касательных		Уравнение изоклины	Примечание
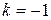
			Так как , мало, то полагаем , тогда
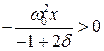
			Это ось абсцисс

Нанесем изоклины на фазовой плоскости. Изоклины и проходят через II и IV квадранты, изоклина – через I и III (так как >0), а ось абсцисс является изоклиной вертикальных касательных (). Хотя число изоклин очень мало, уже удается выяснить характер фазовых траекторий. Пользуясь известной методикой, строим приближенную интегральную кривую (Рис.15).

Видно, что она имеет вид спирали. Точное решение уравнения (3.16) показывает, что интегральная кривая представляет собой логарифмическую спираль (спираль Архимеда) (рисунок 16).

Если взять другое начальное значение, получим другую спираль, не пересекающуюся с первой. Это справедливо и для любых других начальных условий.

Дадим формулировку начальной точки типа фокус.

Особой точкой типа фокус называется точка, которая является асимптотической для интегральных кривых типа спиралей, вложенных друг в друга.

Чтобы интегральная кривая стала фазовой траекторией, необходимо указать направление движения изображающей точки. Воспользуемся уравнением . Если , то согласно правилам математического анализа должно расти, т.е. изображающая точка в верхней полуплоскости движется слева направо, а в нижней – справа налево (, должно уменьшаться). Изображающая точка движется к особой точке, система стремится к состоянию равновесия. Такая особая точка называется устойчивым фокусом.

Имея фазовый портрет линейной системы, мы также можем сопоставить его с поведением системы во времени, так как нам известно точное решение динамического уравнения. Видим, что «затухающая» синусоида соответствует логарифмической спирали. Чем больше затухание, тем шире шаг спирали.

Для линейной системы с помощью фазового портрета можно оценить потери в системе, например логарифмический декремент затухания (логарифм отношения амплитуд за один виток спирали).

Обобщая эти результаты, можно ожидать, что убывающие колебательное движение на фазовой плоскости будет отображаться фазовыми траекториями типа скручивающейся спирали.

Особая точка типа устойчивый фокус соответствует системе с потерями. По мере движения такой системы начальный запас энергии уменьшается, и система стремится к состоянию покоя, состоянию равновесия (рис 17). Факт затухания формально отражается в том, что коэффициент затухания - величина положительная.

В настоящее время известно много систем, которые описываются линейным дифференциальным уравнением с отрицательным «затуханием»:

, (3.23)

где .

Уравнение фазовых траекторий будет

. (3.24)

Если в этом уравнении сделать замену

, (3.25)

то выражение (3.23) примет вид:

, (3.26)

которое по форме точно совпадает с (3.16).

Операция (3.24) представляет зеркальное отображение относительно оси ординат.

Поэтому, при фазовый портрет имеет также вид спиралей, но с учетом движения изображающей точки говорят о раскручивающейся спирали. Изображающая точка уходит от особой точки. Такая особая точка называется неустойчивым фокусом.

Движение во времени будет описываться «нарастающей» синусоидой (рис.18):

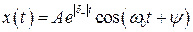. (3.27)

Приведем пример системы, фазовый портрет которой содержит особую точку типа неустойчивый фокус. Рассмотрим самовозбуждение генератора на транзисторе. Сначала получим уравнение такого генератора, а затем исследуем его. Простейшая схема автогенератора приведена на рис. 19. Опишем ее математически.

Обозначим ток индуктивной ветви , емкостной , тогда по законам Кирхгофа имеем два уравнения:

, (3.28)

. (3.29)

На участке база-эмиттер

. (3.30)

Сравним некоторые члены уравнения и попытаемся упростить выражения. Обычно ток базы много меньше любого из других токов схемы, т.е. можно им пренебречь; тогда из уравнений можно исключить члены, содержащие . Например, в уравнении (3.30) можно приберечь вторым членом выражения ввиду его малости:

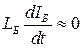. (3.31)

С математической точки зрения это приводит к тому, что понижается порядок уравнения. С физической точки зрения пренебрежение током не приводит к искажению сущности процесса работы генератора. С учетом того, что выражается через и , и, продифференцировав уравнение (3.28), можно записать:

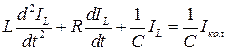. (3.32)

Левая часть уравнения представляет знакомое для нас выражение контура с потерями. В правую часть входит ток коллектора . В общем случае является нелинейной функцией напряжений на базе и коллекторе. Но мы будем предполагать, что переменные сигналы малы и воспользуемся малосигнальными параметрами транзистора. Будем полагать, что

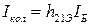, (3.33)

где 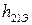– коэффициент передачи по току в схеме с общим эмиттером (выходной проводимостью пренебрегли, так как обычно ). Ток базы и напряжение на базе связаны соотношением:

(3.34)

(внутренней обратной связью в транзисторе пренебрегаем ).

Подставляя в (3.32) соответствующие переменные из (3.30) и (3.34), получим

. (3.35)

С учетом (3.35) уравнение (3.32) примет вид:

, (3.36)

где

, (3.37)

сравнивая с (3.23), получаем

. (3.38)

Величина (что обеспечивается соответствующим включением катушки обратной связи) является необходимым условием . Подбором транзистора с нужными параметрами и регулировкой связи между катушками М можно добиться, чтобы «затухание» стало отрицательным. Фазовый портрет для этого случая мы уже рассмотрели. Если говорить конкретно об LC-генераторе, то неустойчивый фокус описывает процесс самовозбуждения.

Применительно к электрическим цепям нередко пользуются понятием отрицательного сопротивления. В нашем случае формально можно рассматривать как количественную характеристику сопротивления, и получается, что контур имеет как бы два сопротивления: положительное R и отрицательное . Под словом отрицательное сопротивление понимается, что в системе есть вклад энергии по переменному сигналу за счет внешнего постоянного источника.

Поиск по сайту: