Особая точка типа центр

В качестве примера системы, фазовый портрет который содержит особую точку типа центр, рассмотрим гармонический осциллятор. Его динамическое уравнение:

. (3.14)

Получим уравнение фазовой траектории. Для этого запишем динамическое уравнение в стандартной форме:

. (3.15)

Исключим время:

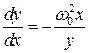. (3.16)

И найдем координаты особой точки

. (3.17)

Рассмотрим поведение фазовых траекторий вблизи особой точки. Решим уравнение (3.16) методом разделения переменных:

. (3.18)

Интегрирую левую и правую части, получим

. (3.19)

Где - постоянная, зависящая от начальных условий. Запишем его в виде

. (3.20)

Мы получили уравнение эллипса. Каждому значению константы С

Особая точка, окруженная эллипсами, является частным случаем особой точки типа центр. В общем случае фазовые траектории могут иметь любую форму. Сформулируем определение центра.

Центром называется изолированная особая точка, окруженная замкнутыми траекториями, вложенная друг в друга.

Как уже указывалось, метод фазовой плоскости является качественным методом исследования систем. Воспользуемся тем, что нам известно точное решение уравнения гармонического осциллятора:

, (3.21)

И у нас есть его фазовый портрет. Посмотрим, какую информацию несет фазовый портрет о движении системы

1) Колебание во времени периодическое. На фазовой плоскости это отображается замкнутой траекторией.

2) Форма колебаний гармонического осциллятора – синусоида, на фазовой плоскости траектория – эллипс.

Можно утверждать: если форма колебаний гармоническая, то на фазовой плоскости фазовые траектории – эллипсы; если фазовые траектории отличаются от эллипса, то колебания не гармонические.

3) С помощью фазовой траектории можно оценить амплитуду колебаний ,но ничего нельзя сказать о периоде колебаний.

Поиск по сайту: