Особая точка типа седло

Рассмотрим в качестве примера маятник в вертикальном положении (Рис.27). Получим динамическое уравнение такой колебательной системы. В общем случае уравнение математического маятника записывается в виде;

. (3.57)

Положим, что угол равен . Тогда при малых углах отклонения от вертикального положения

, (3.58)

И уравнение маятника примет вид:

. (3.59)

Уравнение фазовых траекторий получим по стандартной методике. Динамические уравнения системы запишем в виде:

, (3.60)

. (3.61)

Исключим время

. (3.62)

Особая точка будет: , 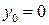(вертикальное положение равновесия).

Интегрируя уравнение с помощью метода разделения переменных имеем;

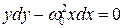, (3.63)

, (3.64)

где – постоянная. Разделим оба уравнения на

. (3.65)

Последнее уравнение есть ни что иное, как уравнение гиперболы в каноническом виде. Картина на фазовой плоскости будет иметь вид, приведенный в рис.28.

Стрелки, указывающие направление движения изображающей точки, проставлены с учетом первого динамического уравнения (3.38).

Семейство гипербол соответствует разным постоянным . При фазовые траектории – прямые . Эти прямые являются ассимтотами для гипербол.

Обобщая полученные результаты, дадим определение особой точки типа седло, для общего случая.

Особая точка типа седло – это точка, через которую проходят две интегральные кривые,, являющиеся асимптотами для кривых типа гипербол.

Фазовый портрет системы с равновесием, соответствующим особой точке типа седло, показывает, что при любых начальных условиях и бесконечном времени наблюдения система уходит от состояния равновесия. Исключение составляют две фазовые траектории (асимптота «а» на рисунке). Если начальная системы соответствует положению изображающей точки на этих траекториях, то система движется к равновесию. Касательно маятника это значит, что в начальный момент мы так отклонили его и сообщили ему такой импульс, что со временем он приходит в состояние вертикального равновесия и остается в нем. Опыт подсказывает, что этого не бывает. Более того, практически невозможно реализовать начальные условия, которые соответствуют точно заданной фазовой траектории.

Систему, у которой состояние равновесия представлено собой точкой типа седло, относят к системе с «отталкивающей силой». В динамическом уравнении

, (3.66)

коэффициент в выражении для упругой силы имеет отрицательный знак. Отсюда и происходит термин «отталкивающая сила». В частности, для математического маятника в вертикальном положении (см. (3.59)) , .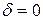

Примером радиотехнической схемы, которая имеет равновесие, отображаемое на фазовой плоскости особой точкой типа седло, является мультивибратор. Выведем уравнение, описывающее процесс самовозбуждения мультивибратора. Покажем, что оно также имеет «отталкивающую силу» . Схема представлена на рисунке 29. По существу – это два каскада усилителя с RC-связями, включенные в кольцо обратной связи.

Считаем, что усилители идеальные. Тогда ,.

Выходные напряжения связаны с входными

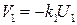, (3.67)

. (3.68)

Составим уравнения методом узловых потенциалов.

Сумма токов в первом узле

. (3.69)

Во втором узле

. (3.70)

Обозначим

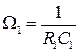; (3.71)

. (3.72)

Подставим (3.67) и (3.68) в (3.69) и (3.70), соответственно. Тогда уравнения примут вид:

. (3.73)

Исключим . Продифференцируем слагаемые второго уравнения (3.73) и умножим все члены на

. (3.74)

Подставляем из первого уравнения (3.73) получим

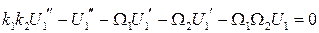, (3.75)

собираем члены одного порядка и, разделив на , получим

. (3.76)

Сравнивая полученное уравнение (3.76) со стандартным (3.66), видим

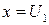, (3.72)

, (3.77)

. (3.78)

Если коэффициент усиления (что всегда реализуется в схеме), то . Появляется «отталкивающая сила» и особая точка будет типа седло.

Поиск по сайту: