Особая точка типа узел

В качестве примера возьмем линейную систему с большим затуханием. Ее уравнение

. (3.39)

Условие большого затухания .

Производя стандартные преобразования, получим уравнение фазовой траектории

. (3.40)

Особая точка , 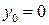расположена в начале координат.

Решив уравнение (3.39) точно или приближенно, можно построить фазовый портрет системы. (В качестве домашнего задания предлагается найти фазовый портрет методом изоклин, как это было сделано для системы с малым затуханием).

Мы получим портрет несколько быстрее, используя точное решение уравнения (2.11). Сразу оговоримся, что такой способ построения фазовой траектории имеет ограниченное применение, так как точное решение динамического уравнения удается найти редко.

Итак, для системы с большим затуханием имеем

, (3.41)

, (3.42)

где – корни характеристического уравнения, действительные и отрицательные.

Рассматриваем уравнение (3.40, 3.41) как параметрическую форму записи фазовой траектории . Чтобы получить функциональную зависимость, исключим параметры время. Умножим все члены первого уравнения (3.40) на ;

(3.43)

и вычтем из (3.42). Получим

. (3.44)

Аналогично получим второе уравнение, умножив выражение (3.41) на

. (3.45)

И вычитая его из (3.44). Получим следующую формулу

. (3.46)

Возведем правую и левую части в степень

. (3.47)

Разделим левые и правые части (3.44) и (3.47) соответственно

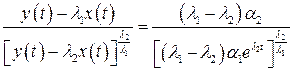. (3.48)

правая часть зависит от начальных условий и параметров системы, т.е. величина постоянная. Обозначим ее С. Тогда

. (3.49)

Это уравнение фазовой кривой в неявном виде. Чтобы выяснить, какие кривые имеют место, произведем аффинное преобразование координат

. (3.50)

При этом топология не нарушается: замкнутые кривые остаются замкнутыми, прямые- прямыми и т.д. Уравнение (3.49) примет вид:

. (3.51)

Учтем, что . В частности, если , то , т.е. получаем семейство парабол, график которых представлен на рис.20. Перейдем к координатам . Ось соответствует и на плоскости перейдет в прямую . Ось 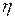перейдет в прямую . Параболы деформируются, но все они проходят через особую точку – начало координат.

Дадим определение особой точки типа узел.

Особая точка, через которую проходят интегральные кривые типа парабол, называется узлом.

Проставив стрелки – указывающие движение системы со временем, получим фазовый портрет системы с большим затуханием (Рис.21).

Если изображающая точка движется к особой, то последняя называется устойчивым узлом.

Имея фазовый портрет колебательной системы с большим затуханием, можно быстро и наглядно проследить роль начальных условий для движения системы. Можно четко выделить три типа движения и три области начальных условий (Рис.22).

1. Изображающая точка движется к особой точке, ни разу не пересекая ни одну из осей. Это будет наблюдаться в областях 1а и 1б (см. на рисунке). В них изображающая точка движется к особой точке, т.е. координата х(t) монотонно убывает; этому соответствует график на следующем рисунке (Рис.23(1))

2. Изображающая точка при движении пересекает ось абсцисс один раз (это означает, что скорость проходит через нуль). Подобная картина может наблюдаться в 1 и 3 квадрантах (обозначено 2а и 2б).

Осциллограмма, соответствующая этому случаю, приведена на втором рисунке (Рис.23(2)).

3. изображающая точка пересекает и ось абсцисс, и ось ординат, т.е. скорость и координата один раз меняют знак. Это соответствует области 3 на самом верхнем рисунке, а осциллограмма для этого случая приведена на самом нижнем рисунке (Рис.23(3)).

Эти типы движения встречаются в системах автоматического регулирования.

Существуют колебательные системы, для которых изображающая точка может уходить от особой точки типа узел. Такой узел называется неустойчивым.

В динамическом уравнении системы

, (3.51)

«затухание» становится отрицательным , но большим по модулю . Интегральные кривые представляют собой зеркальное отображение кривых при 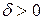относительно оси . В верхней полуплоскости точка движется слева нпараво, в нижней наоборот. Видно, что изображающая точка уходит от положения равновесия (Рис.24).

Осциллограммы имеют вид растущих экспонент (Рис.25).

В качестве примера того, что такие системы существуют, рассмотрим процесс самовозбуждения RC-генератора.

Поиск по сайту: