Устойчивость равновесия линейной системы с N степенями свободы

В общем случае система описывается линейными уравнениями I-го порядка

. (6.23)

Предположим, что , и детерминант, составленный из этих коэффициентов, отличен от нуля

. (6.24)

Уравнение (6.23) является обобщением уравнения (6.9).

В состоянии равновесия все производные равны нулю, так как во времени не изменяется ни одна из координат

. (6.25)

Система уравнений, из которых определяются координаты состояния равновесия, примет вид:

. (6.26)

Поскольку , все координаты равны нулю:

.

Состояние равновесия расположено в начале координат.

Исследуем поведение системы вблизи состояния равновесия.

Найдем точное решение (6.12), пользуясь методом Эйлера. Для любой координаты частное решение есть

, (6.27)

где .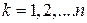

Подставим (6.27) в (6.23)

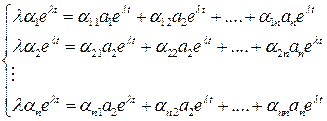, (6.28)

сократим на и соберем коэффициенты при одинаковых :

. (6.29)

Получили систему однородных уравнений относительно , к = 1, …, n. Чтобы хотя бы одно из них было отлично от нуля, нужно чтобы детерминант (6.14) был равен нулю:

. (6.30)

Если раскрыть этот детерминант, собрать коэффициенты при одинаковых степенях , то получим алгебраическое уравнение относительно 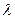(характеристическое уравнение);

, (6.31)

где – постоянные, зависящие от .

Характеристическое уравнение (6.31) в общем случае имеет корней, так как уравнение n -ого порядка; .

Общее решение для любой координаты есть суперпозиция частных:

. (6.32)

постоянных а_km (m = 1, 2, …, n) независимы и определяются начальными условиями. Остальные постоянные связаны между собой уравнениями (6.29).

Из общего решения (6.32) видно, что поведение координат со временем определяется экспонентами .

В общем случае корни комплексные

, где . (6.33)

Если хотя бы одно значение δ_m > 0, соответствующая экспонента стремится к бесконечности, следовательно ξ _k (t) → ∞ при t → ∞; система уходит от положения равновесия. Состояние равновесия неустойчиво. Если все вещественные части корней отрицательны (δ_m < 0, m = 1, …, n), то в этом случае ξ_k (t! → 0) при t → ∞, т.е. система стремится перейти в положение равновесия. Состояние равновесия абсолютно устойчиво.

Если вещественные части хотя бы у одной пары комплексно-сопряженных корней равны нулю, а остальные δ_m < 0, то частным решением системы (6.12) будет гармоническое колебание. Система будет совершать движение около положения равновесия, не достигая его. Состояние равновесия устойчиво по Ляпунову.

В результате анализа можно сделать вывод: для того, чтобы оценить устойчивость равновесия линейной системы, не обязательно знать корни характеристического уравнения (6.16); достаточно иметь сведения о знаках вещественных частей корней.

Для этой цели служит критерий Рауса-Гурвица. Он устанавливает необходимые и достаточные условия того, чтобы реальные части всех корней характеристического уравнения были отрицательными. В этом случае состояние равновесия системы абсолютно устойчиво.

Пусть характеристическое уравнение имеет вид:

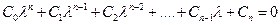. (6.34)

(В нашем случае (6.31) ).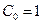

1. Необходимым условием того, чтобы вещественные части корней характеристического уравнения были отрицательны, является требование: все коэффициенты характеристического уравнения должны быть положительны. Если хотя бы один из этих коэффициентов отрицателен, то обязательно найдется хотя бы один корень с положительной реальной частью и состояние равновесия будет неустойчивым.

2. Для формулирования достаточного условия необходимо их коэффициентов уравнения (6.19) составить матрицу Гурвица. Правило составления матрица следующее;

. (6.35)

Матрица квадратная. Диагональными элементами являются коэффициенты уравнения (6.34), начиная с . В строках матрицы записываются коэффициенты: с убывающими номерами вправо от диагонали, с возрастающими – влево. Если соответствующие коэффициенты отсутствуют, записывают нули.

Матрица Гурвица для (6.34) имеет вид:

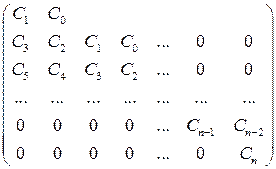. (6.36)

Достаточным условием того, чтобы вещественные части корней характеристического уравнения были отрицательными, является выполнение следующих неравенств:

, (6.37)

(6.38)

6.39)

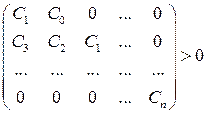. (6.40)

т.е. диагональные миноры определителя Гурвица должны быть положительными.

Поиск по сайту: