Абсолютно неупругий удар. Абсолютно упругий удар. Скорости шаров после абсолютно упругого центрального удара

Абсолютно неупругий удар - соударение двух тел, в результате которого тела соединяются, двигаясь дальше как единое целое. Абсолютно неупругий удар можно продемонстрировать с помощью шаров из пластилина (глины), которые движутся навстречу друг другу.

Если массы шаров m₁ и m₂, их скорости до удара ν₁ и ν₂, то, используя закон сохранения импульса

где v - скорость движения шаров после удара. Тогда

(15.10)
В случае движения шаров навстречу друг другу они вместе будут продолжать движение в ту сторону, в которую двигался шар с большим импульсом. В частном случае, если массы шаров равны (m₁=m₂), то

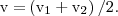
Определим, как изменяется кинетическая энергия шаров при центральном абсолютно неупругом ударе. Так как в процессе соударения шаров между ними действуют силы, зависящие от их скоростей, а не от самих деформаций, то мы имеем дело с дисипативными силами, подобным силам трения, поэтому закон сохранения механической энергии в этом случае не должен соблюдаться. Вследствие деформации происходит уменьшение кинетической энергии, которая переходит в тепловую или другие формы энергии. Это уменьшение можно определить по разности кинетической энергии тел до и после удара:

Используя (10), получаем

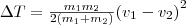
Если ударяемое тело было первоначально неподвижно (ν₂=0), то

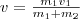
и

Когда m₂>>m₁ (масса неподвижного тела очень велика), то ν << ν₁ и практически вся кинетическая энергия тела переходит при ударе в другие формы энергии. Поэтому, например, для получения значительной деформации наковальня должна быть значительно массивнее молота. Наоборот, при забивании гвоздей в стену масса молота должна быть гораздо большей (m₁>>m₂), тогда ν≈ν₁ и почти вся энергия тратится на возможно большее перемещение гвоздя, а не на остаточную деформацию стены.
Абсолютно неупругий удар - это пример потери механической энергии под действием диссипативных сил.

Абсолютно упругий удар - соударение двух тел, в результате которого в обоих участвующих в столкновении телах не остается никаких деформаций и вся кинетическая энергия тел до удара после удара снова превращается в первоначальную кинетическую энергию (отметим, что это идеализированный случай).

Для абсолютно упругого удара выполняются закон сохранения кинетической энергии и закон сохранения импульса.

Обозначим скорости шаров массами m₁ и m₂ до удара через ν₁ и ν₂, после удара - через ν₁' и ν₂' (рис. 1). Для прямого центрального удара векторы скоростей шаров до и после удара лежат на прямой линии, проходящей через их центры. Проекции векторов скоростей на эту линию равны модулям скоростей. Их направления учтем знаками: положительное соотнесем движению вправо, отрицательное - движению влево.

При указанных допущениях законы сохранения имеют вид
(1)
(2)
Произведя соответствующие преобразования в выражениях (1) и (2), получим
(3)
(4)
откуда

(5)
Решая уравнения (3) и (5), находим
(6)

(7)
Разберем несколько примеров.
1. При ν₂ =0

(8)
(9)
Проанализируем выражения (8) в (9) для двух шаров различных масс:
а) m₁=m₂. Если второй шар до удара висел неподвижно (ν₂ =0) (рис. 2), то после удара остановится первый шар (ν₁' =0), а второй будет двигаться с той же скоростью и в том же направлении, в котором двигался первый шар до удара (ν₂' = ν₁);

б) m₁>m₂. Первый шар продолжает двигаться в том же направлении, как и до удара, но с меньшей скоростью (ν₁' < ν₁). Скорость второго шара после удара больше, чем скорость первого после удара (ν₂' > ν₁') (рис. 3);

в) m₁<m₂. При ударе направление движения первого шара изменяется - шар отскакивает обратно. При этом второй шар движется в сторону, в которую двигался первый шар до удара, но с меньшей скоростью, т. е. ν₂' < ν₁ (рис. 4);

г) m₂>>m₁ (например, столкновение шара со стеной). Из уравнений (8) и (9) следует, что ν₁' = - ν₁; ν₂' ≈ 2m₁ ν₂' /m₂.
2. При m₁=m₂ выражения (6) и (7) будут иметь вид ν₁' = ν₂; ν₂' = ν₁; т. е. шары равной массы как бы обмениваются скоростями.

Момент импульса частицы относительно точки и относительно оси. Момент силы относительно точки и относительно оси. Законы изменения и сохранения момента импульс системы. Момент импульса твердого тела, вращающегося относительно неподвижной оси. Момент инерции тела относительно оси. Вычисление моментов инерции стержня, сплошного цилиндра. Теорема Гюйгенса-Штейнера. Закон сохранения момента импульса для вращательного движения.

Моментом импульса (количества движения) материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произведением:

где r - радиус-вектор, проведенный из точки О в точку A, p =m v - импульс материальной точки (рис. 1); L - псевдовектор, направление которого совпадает с направлением поступательного движения правого винта при его вращении от r к р.

Модуль вектора момента импульса

где α - угол между векторами r и р, l - плечо вектора р относительно точки О.

Моментом импульса относительно неподвижной оси z называется скалярная величина L_z, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси. Момент импульса L_z не зависит от положения точки О на оси z.

При вращении абсолютно твердого тела вокруг неподвижной оси z каждая точка тела движется по окружности постоянного радиуса r_iсо скоростью v_i. Скорость v_i и импульс m_iv_i перпендикулярны этому радиусу, т. е. радиус является плечом вектора m_iv_i. Значит, мы можем записать, что момент импульса отдельной частицы равен

(1)

и направлен по оси в сторону, определяемую правилом правого винта.

Монет импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц:

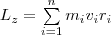
Используя формулу v_i = ωr_i, получим

т. е. 2)

Таким образом, момент импульса твердого тела относительно оси равен моменту инерции тела относительно той же оси, умноженному на угловую скорость. Продифференцируем уравнение (2) по времени:

т. е.

Эта формула - еще одна форма уравнения динамики вращательного движения твердого тела относительно неподвижной оси: производная момента импульса твердого тела относительно оси равна моменту сил относительно той же оси.

Можно показать, что имеет место векторное равенство

(3)
В замкнутой системе момент внешних сил и откуда

(4)

Выражение (4) представляет собой закон сохранения момента импульса: момент импульса замкнутой системы сохраняется, т. е. не изменяется с течением времени.

Закон сохранения момента импульса также как и закон сохранения энергии является фундаментальным законом природы. Он связан со свойством симметрии пространства - его изотропностью, т. е. с инвариантностью физических законов относительно выбора направления осей координат системы отсчета (относительно поворота замкнутой системы в пространстве на любой угол).

Здесь мы продемонстрируем закон сохранения момента импульса с помощью скамьи Жуковского. Человек, сидящий на скамье, вращающаяся вокруг вертикальной оси, и держащий в вытянутых руках гантели (рис. 2), вращается внешним механизмом с угловой скоростью ω₁. Если человек прижмет гантели к телу, то момент инерции системы уменьшится. Но момент внешних сил равен нулю, момент импульса системы сохраняется и угловая скорость вращения ω₂ увеличивается. Аналогичным образом, гимнаст во время прыжка через голову поджимает к туловищу руки и ноги, с целью уменьшить свой момент инерции и тем самым увеличить угловую скорость вращения.

Сопоставим основные величины и уравнения, определяющие вращение тела вокруг неподвижной оси и его поступательное движение (см таблицы ниже).

Моментом силы F относительно неподвижной точки О называется физическая величина, определяемая векторным произведением радиуса-вектора r, проведенного из точки О в точку А приложения силы, на силу F (рис. 1):

Здесь М - псевдовектор, направление которого совпадает с направлением поступательного движения правого винта при его вращении от r к F. Модуль момента силы

(1)

где α - угол между r и F; rsinα= l - наименьшее расстояние между линией действия силы и точкой О - плечо силы.

Моментом силы относительно неподвижной оси z называется скалярная величина M_z, равная проекции на эту ось вектора М момента силы, определенного относительно произвольной точки О данной оси z (рис. 2).

Рис.2

Значение момента М_z не зависит от выбора положения точки О на оси z.
Если ось z совпадает с направлением вектора М, то момент силы представляется в виде вектора, совпадающего с осью:

Найдем выражение для работы при вращении тела (рис.3).

Рис.3

Пусть сила F приложена в точке В, находящейся от оси z на расстоянии r, α - угол между радиусом-вектором r и направлением силы. Так как тело абсолютно твердое, то работа этой силы равна работе, которую необходимо затратить на поворот всего тела. При повороте тела на бесконечно малый угол dφ точка приложения В проходит путь ds=rdφ и работа равна произведению проекции силы на направление с мещения на величину смещения:

(2)

Учитывая (1), можем записать

где Frsinα=F l =M_z - момент силы относительно оси z. Значит, работа при вращении тела равна произведению момента действующей силы на угол поворота.
Работа при вращении тела идет на увеличение его кинетической энергии: dA=dT, но поэтому , или
Учитывая, что получаем

(3)

Уравнение (3) представляет собой уравнение динамики вращательного движения твердого тела относительно неподвижной оси.
Можно показать, что если ось z совпадает с главной осью инерции, проходящей через центр масс, то имеет место векторное равенство

где J - главный момент инерции тела (момент инерции относительно главной оси).

Момент инерции

Моментом инерции системы (тела) относительно данной оси называется физическая величина, равная сумме произведений масс n материальных точек системы на квадраты их расстояний до рассматриваемой оси:

В случае непрерывного распределения масс эта сумма сводится к интегралу

где интегрирование производится по всему объему тела. При этом величина r в есть функция положения точки с координатами х, у, z. В качестве примера будем искать момент инерции однородного сплошного цилиндра высотой h и радиусом R относительно его геометрической оси (рис. 1).

Рис.1

Разобьем цилиндр на отдельные полые концентрические цилиндры бесконечно малой толщины dr с внутренним радиусом r и внешним r+dr. Момент инерции отдельного полого цилиндра dJ=r²dm (так как dr<<r, то считаем, что расстояние всех точек цилиндра от оси равно r), где dm - масса всего элементарного цилиндра; его объем 2πrhdr. Если ρ-плотность материала, то dm=2πrhρdr и dJ=2πhρr³dr. Тогда момент инерции сплошного цилиндра

но так как πR2h - объем цилиндра, то его масса m=πR2hρ, а момент инерции

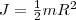
Если мы знаем момент инерции тела относительно оси, проходящей через его центр масс, то мы можем найти и момент инерции относительно любой другой параллельной этой оси, который можно найти с помощью теоремы Гюйгенса-Штейнера: момент инерции тела J относительно произвольной оси равен моменту его инерции J_c относительно параллельной оси, проходящей через центр масс С тела, сложенному с произведением массы m тела на квадрат расстояния а между осями:

Приведем значения моментов инерции (табл. 1) для некоторых тел (тела считаются однородными, m - масса тела).

Поиск по сайту: