АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Основные уравнения динамики вращательного движения твердого тела

Читайте также:
  1. I. ОСНОВНЫЕ ПОНЯТИЯ (ТЕРМИНЫ) ЭКОЛОГИИ. ЕЕ СИСТЕМНОСТЬ
  2. I.3. Основные этапы исторического развития римского права
  3. II Съезд Советов, его основные решения. Первые шаги новой государственной власти в России (октябрь 1917 - первая половина 1918 гг.)
  4. II. Основные задачи и функции
  5. II. Основные показатели деятельности лечебно-профилактических учреждений
  6. II. Основные проблемы, вызовы и риски. SWOT-анализ Республики Карелия
  7. II. ОСНОВЫ МОЛЕКУЛЯРНОЙ ФИЗИКИ И ТЕРМОДИНАМИКИ
  8. IV. Механизмы и основные меры реализации государственной политики в области развития инновационной системы
  9. VI.3. Наследственное право: основные институты
  10. А — при двустороннем движении судов; б — при одностороннем движения
  11. А) возникновение и основные черты
  12. А) ОСНОВНЫЕ УСЛОВИЯ ВЕРНОЙ ПЕРЕДАЧИ СЛОВ, ОБОЗНАЧАЮЩИХ НАЦИОНАЛЬНО-СПЕЦИФИЧЕСКИЕ РЕАЛИИ

Основной закон динамики вращательного движения можно получить из второго закона Ньютона для поступательного движения твердого тела

, (1.6)

где F – сила, приложенная к телу массой m; а – линейное ускорение тела.

Если к твердому телу массой m в точке А (рис. 5) приложить силу F, то в результате жесткой связи между всеми материальными точками тела все они получат угловое ускорение 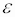и соответственные линейные ускорения, как если бы на каждую точку действовала сила . Для каждой материальной точки можно записать:

,

где , поэтому

, (1.7)

где mi – масса i- й точки; 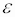– угловое ускорение; ri – ее расстояние до оси вращения.

Умножая левую и правую части уравнения (1.7) на ri, получают

, (1.8)

где – момент силы – это произведение силы на ее плечо .

Плечом силы называют кратчайшее расстояние от оси вращения “ОО” (рис. 5) до линии действия силы .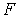

Рис. 5. Твердое тело, вращающееся под

действием силы F около оси “ОО”

– момент инерции i -й материальной точки.

Выражение (1.8) можно записать так:

. (1.9)

Просуммируем левую и правую части (1.9) по всем точкам тела:

.

Обозначим через М, а через J, тогда

(1.10)

Уравнение (1.10) – основной закон динамики вращательного движения твердого тела. Величина – геометрическая сумма всех моментов сил, то есть момент силы F, сообщающий всем точкам тела ускорение . – алгебраическая сумма моментов инерции всех точек тела. Закон формулируется так: «Момент силы, действующий на вращающееся тело, равен произведению момента инерции тела на угловое ускорение».

Мгновенное значение углового ускорения , есть первая производная угловой скорости по времени , то есть

, (1.11)

где – элементарное изменение угловой скорости тела за элементарный промежуток времени .

Если в выражение основного закона (1.10) поставить значение мгновенного ускорения (1.11), то

или , (1.12)

где – импульс момента силы – это произведение момента силы на промежуток времени .

– изменение момента импульса тела, – момент импульса тела есть произведение момента инерции J на угловую скорость , а есть .

Поэтому основной закон динамики вращательного движения твердого тела формулируется так: “Импульс момента силы 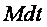, действующий на вращательное тело, равен изменению его момента импульса ”:

или


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)