АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Сложение двух гармонических колебаний одинакового направления и частоты. Геометрическая интерпретация

Читайте также:
  1. I. Порядок медицинского отбора и направления на санаторно-курортное лечение взрослых больных (кроме больных туберкулезом)
  2. IV. Приоритетные направления деятельности Правительства Республики Карелия на период до 2017 года
  3. Амплитуда, период, частота, фаза колебаний.
  4. Анализ зарегистрированных Web-страниц по следующим направлениям
  5. Анализ сезонных колебаний
  6. Анализ сезонных колебаний товарооборота
  7. Анализ спинномозговой жидкости и ее клиническая интерпретация.
  8. Аналитические возможности, задачи и основные направления анализа СНС
  9. Архитектура XXв. Основные направления и стили.
  10. Безопасность технологического оборудования: классификация, требования безопасности и основные направления обеспечения безопасности
  11. Билет № 22 Философский иррационализм: основные идеи и направления.
  12. Билет № 35 Проблема познания в философии. Основные направления в теории познания.

При сложении двух гармонических колебаний одинакового направления и частоты, результирующее смещение будет суммой () смещений и , которые запишутся следующими выражениями:

, ,
Сумма двух гармонических колебаний также будет гармоническим колебанием той же круговой частоты:
= .
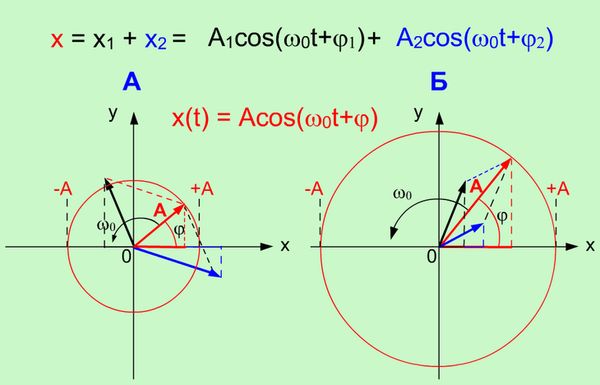
Значения амплитуды А и начальной фазы φ этого гармонического колебания будет зависеть от амплитуд исходных колебаний и их начальных фаз (Рис. 1.2).

Рисунок 1.2. Сложение двух гармонических колебаний одинакового направления и частоты

На рисунке 1.2. приведено два примера А и В сложения гармонических колебаний с использованием метода векторных диаграмм. Из векторных диаграмм видно, что направление (начальная фаза φ) и длина А вектора амплитуды суммарного гармонического колебания зависит, как от направления (от начальных фаз), так и от длины векторов амплитуд исходных гармонических колебаний.
Если угол (разность фаз: Δφ = φ1 - φ2) между векторами А1 и А2 равен 0, то исходные колебания находятся в фазе и суммарная амплитуда (А =А1 +А2) будет максимальна. Если угол (разность фаз: Δφ = φ1 - φ2) между векторами А1 и А2 равен - π или π, то исходные колебания находятся в противофазе и суммарная амплитуда (А = А1 -А2 ) будет минимальна.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)