АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
|
Рассмотрим далее решение некоторых типовых задач
Задача 1. Уравнение прямой, проходящей через две заданные точки.
       Пусть имеются две точки М1(x 1, y 1) и М2(x 2, y 2). Из геометрических соображений (рис. 2) угловой коэффициент искомой прямой равен Пусть имеются две точки М1(x 1, y 1) и М2(x 2, y 2). Из геометрических соображений (рис. 2) угловой коэффициент искомой прямой равен  . Подставим полученное значение k в уравнение (3): y = . Подставим полученное значение k в уравнение (3): y =  x +b. x +b.
Рис. 2 Учитывая, что прямая проходит через точку М1(x 1, y 1), а, значит, ее координаты удовлетворяют искомому уравнению прямой, находим
b= y 1 -  x 1. x 1.
Окончательно уравнение прямой, проходящей через две заданные точки, записываем в виде
 = = 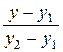 . (4) . (4)
Пример 3. Составить уравнение прямой, проходящей через точки А(1,2) и В(-1,3).
Решение. Искомое уравнение, согласно (4), имеет вид  , откуда x + 2 y - 5 = 0. ■ , откуда x + 2 y - 5 = 0. ■
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | Поиск по сайту:
|






 Пусть имеются две точки М1(x 1, y 1) и М2(x 2, y 2). Из геометрических соображений (рис. 2) угловой коэффициент искомой прямой равен
Пусть имеются две точки М1(x 1, y 1) и М2(x 2, y 2). Из геометрических соображений (рис. 2) угловой коэффициент искомой прямой равен  . Подставим полученное значение k в уравнение (3): y =
. Подставим полученное значение k в уравнение (3): y =  x +b.
x +b.
 x 1.
x 1. =
= 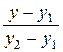 . (4)
. (4) , откуда x + 2 y - 5 = 0. ■
, откуда x + 2 y - 5 = 0. ■