 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Альтернативные возможности производства масла и пушек
Управляемая самостоятельная работа студентов осуществляется в процессе освоения ими дисциплины по представленным ниже темам.



 ТЕМА 2. ТЕХНОЛОГИЯ УПРАВЛЕНИЕ РИСКОМ Контрольные вопросы по теме:
ТЕМА 2. ТЕХНОЛОГИЯ УПРАВЛЕНИЕ РИСКОМ Контрольные вопросы по теме:
1. Принципы и функции управления рисками.
2. Схема процесса риск-менеджмента.
3. Стратегии риск-менеджмента.
4. Стратегии предпринимательского поведения в условиях
риска и неопределенности.
5. Методы управления рисками.
6. Приемы снижения риска и минимизации потерь.
Литература: [1], с. 29-38, 76-108; [3], с. 281-298, 323-373; [6, 7, 11, 13, 18, 20-23, 25, 27].
Форма конт роля: тест.
ТЕМА 3. АНАЛИЗ И ОЦЕНКА РИСКА
Контрольные вопросы по теме:
1. Сущность и область применения вероятностных методов.
2. Сущность и область применения экспертных методов.
3. Сущность и область применения метода аналогов.
4. Сущность и область применения сценарных методов.
5. Сущность и область применения метода построения де
рева решений.
6. Сущность и область применения имитационных методов.
7. Сущность и область применения анализа показателей пре
дельного уровня.
8. Сущность и область применения анализа чувствитель
ности.
9. Сущность и область применения метода ставки процента
с поправкой на риск.
10. Сущность и область применения стохастических мето
дов.
Литература: [1], с. 39-75; [2], с. 43-78; [3], с. 298-323; [5], с. 61-99; [7-9, 11-17, 19, 21, 23, 27].'
Ф орма контрол я: реш ение типовых задач.
1. Фирма планирует организацию одного из коммерческих проектов. Известны экспертные оценки ожидаемой среднегодовой прибыли от реализации шести альтернативных проектов. Выбрать рациональный вариант коммерческого проекта при условии, что среднегодовая прибыль должна быть не менее 45 млн руб. при минимальном риске.
Таблица 2.6.1 - Оценка прибыли по проектам, млн руб.
| Оценка прибыли | Проект | |||||
| 4 п | ||||||
| Минимальная | ||||||
| Максимальная | ■ |
2. На основе анализа безубыточности выбрать вариант про
изводственной программы, минимизирующий предприниматель
ский риск. В первом случае планируется производство 10 тыс. шт.
изделия А, себестоимость которого составляет 15 рублей, а цена
реализации 25 рублей. Второй вариант программы предполагает
производство изделия В в количестве 3 тыс. шт., себестоимость
которого составляет 160 рублей, а цена реализации 200 рублей.
Постоянные издержки фирмы равны 80 тыс. руб.
3. Фирма планирует выход на новый рынок сбыта своего
товара. Затраты на исследование рынка составят 1000 у.е. Доста
точный уровень спроса на рынке прогнозируется с вероятностью
0, 4. При выходе на такой рынок планируется получение прибыли
в размере 2 000 у.е. в год. При отсутствии спроса есть возмож
ность его формирования и развития, общей стоимостью кампа
нии 5 000 у.е. При этом провал компании ожидается с вероятнос
тью 0, 2. В противном случае, сформированный спрос даст воз
можность получения прибыли в размере 2500 у.е. в год. Расчет
ный период 3 года. Проанализировать риск данного решения на
основе построения дерева решений.
4. Известно, что при вложении капитала в мероприятие А из
100 случаев прибыль 300 млн руб. была получена в 25 случаях,


 прибыль 250 млн руб. была получена в 60 случаях и прибыль 320 млн руб. - в 15 случаях. Аналогично, при вложении капитала в мероприятие В прибыль 430 млн руб. была получена с вероятностью 0,2, 300 млн руб. - с вероятностью 0,7 и 250 млн руб. - с вероятностью 0, 1. Определить:
прибыль 250 млн руб. была получена в 60 случаях и прибыль 320 млн руб. - в 15 случаях. Аналогично, при вложении капитала в мероприятие В прибыль 430 млн руб. была получена с вероятностью 0,2, 300 млн руб. - с вероятностью 0,7 и 250 млн руб. - с вероятностью 0, 1. Определить:
- среднее ожидаемое значение прибыли по вариантам;
- дисперсию и среднее квадратическое отклонение;
- коэффициент вариации.
ТЕМА 4. СТРАХОВАНИЕ КАК ОСНОВНОЙ ПРИЕМ РИСК-МЕНЕДЖМЕНТА
Контрольные вопросы по теме:
1. Личное страхование.
2. Имущественное страхование.
3. Страхование ответственности.
4. Перестрахование.
5. Пропорциональное страхование.
6. Непропорциональное страхование.
7. Распределение страховой ответственности.
Литература: [2], с. 170-178; [3], с. 340-358; [4], с. 106-153; [5-6, 10, 19].
Форма контроля: тест.
 ТЕМА 6. ПОДСИСТЕМА РИСК-МЕНЕДЖМЕНТА В ОБЩЕЙ СИСТЕМЕ УПРАВЛЕНИЯ
ТЕМА 6. ПОДСИСТЕМА РИСК-МЕНЕДЖМЕНТА В ОБЩЕЙ СИСТЕМЕ УПРАВЛЕНИЯ
Контрольные вопросы по теме:
1. Содержание функции риск-менеджмента.
2. Рисковый профиль организации.
3. Формирование системы управления рисками.
4. Оценка системы риск-менеджмента.
5. Формирование рискового менталитета.
6. Структуры служб риск-менеджмента.
Литература: [2], с. 135-168, 192-203; [22, 26]. Форма контроля: тест и выполнение контрольного зад ания.
Контрольное задание: выработать рекомендации риск-менеджмента по группам рисков на условном предприятии.
Таблица 2.6.2 — Классификация рисков предприятия
| № | Виды риска | Способ минимизации | Рекомендации |
| Производственные | |||
| Неоптимальное распределение ресурсов | Снижение через предупредительные мероприятия | ||
| Ошибки менеджеров | Снижение... | ||
| Недовольство работников | Снижение... | ____________ | |
| Пожар, стихийные бедствия | Передача страховщику | ||
| 5 6 | Дорожно-транспортные происшествия | Передача... | |
| Уничтожение или порча груза при транспортировке | Передача... | ||
| Потери от небрежности работников | Передача... | ||
| Материальный или моральный ущерб из-за нечестности служащих | Передача... | ||
| Ущерб из-за невыполнения своих обязанностей работником или группой работников | Передача... | ||
| Приостановка деловой активности 1 | Передача... |
 Продолжение таблицы 2.6.2
Продолжение таблицы 2.6.2
Окончание таблицы 2.6.2
 | ||||
 | ||||
 |
| Смерть или заболевание руководителя или ключевого работника | Передача... | ||
| Финансовые | |||
| Неправильное соотношение показателей финансовой деятельности | Снижение... | ||
| Пассивность капиталов или чрезмерно высокая их концентрация | Снижение... | ||
| Невозможность погашения кредитных средств | Передача... | ||
| Увеличение процента налогообложения | Передача... | ||
| 16 Невыполнение договорных обязательств | Передача... | ||
| Инвестиционные | |||
| Невозврат инвестированных средств | Передача... | ||
| Понижение депозитных ставок | Передача... | ||
| Некачественный Снижение... инвестиционный проект;; | |||
| Рыночные | |||
| Экономические колебания и изменения спроса | Снижение... |
| 3! 4 | |||
| Действия конкурентов | IIСнижение... ! | ||
| Изменение цен и уровня прибыли | Снижение... | ||
| Неправильно выбранный проект (вид деятельности) | |||
| Политические | |||
| Политические события, имеющие тяжелые последствия для данного бизнеса | Снижение... |
ЛИТЕРАТУРА
1. Турчак Л.И., Плотников П.В. Основы численных методов. – М.: Физматлит, 2002.
2. Численные методы / Лапчик М.П., Рагулина М.И., Хеннер Е.К. М.: Издат. центр «Академия», 2004.
3. Приближенное решение нелинейных уравнений: Метод. указания / КХТИ. Сост. А.В. Садыков, Казань, 1991.
4. Некоторые методы решения задачи аппроксимации: Метод. указания / Казан. гос. технол. ун-т. Сост. А.Г. Багоутдинова, Т.А. Хрузина, Казань, 2000.
Вариант 2
1. Отделить корни уравнения графически и уточнить один из них методом касательных с точностью  =0,001.
=0,001.
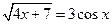
2. Решить систему нелинейных уравнений методом Ньютона с точностью  . Начальное приближение определить графическим способом.
. Начальное приближение определить графическим способом.

3. Решить систему линейных уравнений с трехдиагональной матрицей методом прогонки
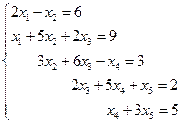
4. Решить систему линейных уравнений методом Зейделя с точностью  .
.
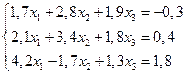
5. Функция задана таблично:

| 1,5 | 2,5 | |||

| 0,2 | 1,8 | 2,4 | 2,2 |
Построить интерполяционный полином Лагранжа для этой функции. С помощью этого полинома найти приближенное значение функции в точке 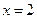 .
.
6. Построить интерполяционный полином Ньютона для функции, заданной таблично:

| 0,1 | 0,5 | 0,9 | 1,3 | 1,7 |

| 1,3 | 1,7 | 2,8 | 3,2 | 2,9 |
С помощью этого полинома найти приближенное значение функции при 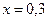 .
.
7. Вычислить определенный интеграл методами прямоугольников, трапеций и парабол при 
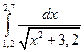
8. Функция задана таблично

| 0,5 | 1,5 | 4,5 | ||||

| 2,61 | 5,49 | 7,02 | 10,10 | 13,11 | 14,6 | 16,12 |
Построить аппроксимирующую прямую 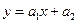 , используя метод наименьших квадратов (решить сначала вручную, затем с помощью программы).
, используя метод наименьших квадратов (решить сначала вручную, затем с помощью программы).
9. Дана задача Коши для обыкновенного дифференциального уравнения I порядка:
 (
( – номер варианта)
– номер варианта)
Найти численное решение задачи методами Эйлера и Рунге-Кутта при  .
.
10. Найти численное решение краевой задачи
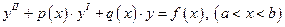
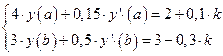
методом конечных разностей
а) вручную: при 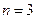 ;
;
б) с помощью программы: при  .
.
Здесь
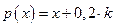 ;
; 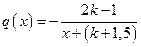 ;
; 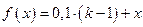
 ;
;  ;
;  – номер варианта
– номер варианта
ЛИТЕРАТУРА
1. Турчак Л.И., Плотников П.В. Основы численных методов. – М.: Физматлит, 2002.
2. Численные методы / Лапчик М.П., Рагулина М.И., Хеннер Е.К. М.: Издат. центр «Академия», 2004.
3. Приближенное решение нелинейных уравнений: Метод. указания / КХТИ. Сост. А.В. Садыков, Казань, 1991.
4. Некоторые методы решения задачи аппроксимации: Метод. указания / Казан. гос. технол. ун-т. Сост. А.Г. Багоутдинова, Т.А. Хрузина, Казань, 2000.
Вариант 3
1. Отделить корни уравнения графически и уточнить один из них методом итераций с точностью  =0,001.
=0,001.
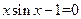
2. Решить систему нелинейных уравнений методом Ньютона с точностью  . Начальное приближение определить графическим способом.
. Начальное приближение определить графическим способом.
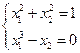
3. Решить систему линейных уравнений с трехдиагональной матрицей методом прогонки
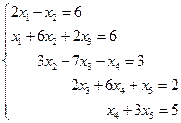
4. Решить систему линейных уравнений методом Зейделя с точностью  .
.
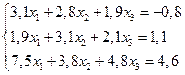
5. Функция задана таблично:

| 0,5 | 1,5 | |||

| 0,4 | 0,8 | 1,7 | 2,6 | 2,4 |
Построить интерполяционный полином Лагранжа для этой функции. С помощью этого полинома найти приближенное значение функции в точке 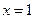 .
.
6. Построить интерполяционный полином Ньютона для функции, заданной таблично:

| 0,1 | 0,3 | 0,5 | 0,7 | 0,9 |

| 2,4 | 2,8 | 3,4 | 3,9 | 3,7 |
С помощью этого полинома найти приближенное значение функции при 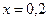 .
.
7. Вычислить определенный интеграл методами прямоугольников, трапеций и парабол при 
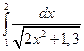
8. Функция задана таблично

| 1,5 | 4,5 | |||||

| 1,91 | 3,12 | 5,91 | 8,11 | 9,10 | 10,11 | 12,10 |
Построить аппроксимирующую прямую 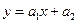 , используя метод наименьших квадратов (решить сначала вручную, затем с помощью программы).
, используя метод наименьших квадратов (решить сначала вручную, затем с помощью программы).
9. Дана задача Коши для обыкновенного дифференциального уравнения I порядка:
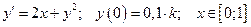 (
( – номер варианта)
– номер варианта)
Найти численное решение задачи методами Эйлера и Рунге-Кутта при  .
.
10. Найти численное решение краевой задачи
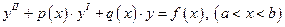
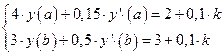
методом конечных разностей
а) вручную: при 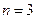 ;
;
б) с помощью программы: при  .
.
Здесь
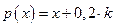 ;
; 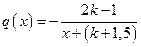 ;
; 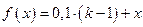
 ;
;  ;
;  – номер варианта
– номер варианта
ЛИТЕРАТУРА
1. Турчак Л.И., Плотников П.В. Основы численных методов. – М.: Физматлит, 2002.
2. Численные методы / Лапчик М.П., Рагулина М.И., Хеннер Е.К. М.: Издат. центр «Академия», 2004.
3. Приближенное решение нелинейных уравнений: Метод. указания / КХТИ. Сост. А.В. Садыков, Казань, 1991.
4. Некоторые методы решения задачи аппроксимации: Метод. указания / Казан. гос. технол. ун-т. Сост. А.Г. Багоутдинова, Т.А. Хрузина, Казань, 2000.
Вариант 4
1. Отделить корни уравнения графически и уточнить один из них методом касательных с точностью  =0,001.
=0,001.
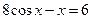
2. Решить систему нелинейных уравнений методом Ньютона с точностью  . Начальное приближение определить графическим способом.
. Начальное приближение определить графическим способом.
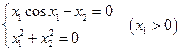
3. Решить систему линейных уравнений с трехдиагональной матрицей методом прогонки

4. Решить систему линейных уравнений методом Зейделя с точностью  .
.
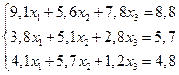
5. Функция задана таблично:

| 1,5 | 2,4 | 4,5 | ||

| 1,7 | 2,6 | 3,2 | 3,8 | 3,7 |
Построить интерполяционный полином Лагранжа для этой функции. С помощью этого полинома найти приближенное значение функции в точке 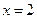 .
.
6. Построить интерполяционный полином Ньютона для функции, заданной таблично:

| 0,2 | 0,4 | 0,6 | 0,8 | 1,0 |

| 2,1 | 2,5 | 3,1 | 3,9 | 3,7 |
С помощью этого полинома найти приближенное значение функции при 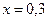 .
.
7. Вычислить определенный интеграл методами прямоугольников, трапеций и парабол при 
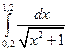
8. Функция задана таблично

| 2,5 | 5,5 | |||||

| 3,9 | 4,91 | 5,89 | 7,95 | 9,90 | 10,94 | 11,86 |
Построить аппроксимирующую прямую 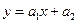 , используя метод наименьших квадратов (решить сначала вручную, затем с помощью программы).
, используя метод наименьших квадратов (решить сначала вручную, затем с помощью программы).
9. Дана задача Коши для обыкновенного дифференциального уравнения I порядка:
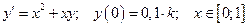 (
( – номер варианта)
– номер варианта)
Найти численное решение задачи методами Эйлера и Рунге-Кутта при  .
.
10. Найти численное решение краевой задачи
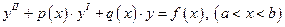
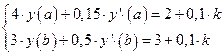
методом конечных разностей
а) вручную: при 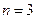 ;
;
б) с помощью программы: при  .
.
Здесь
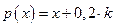 ;
; 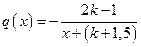 ;
; 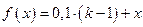
 ;
;  ;
;  – номер варианта
– номер варианта
ЛИТЕРАТУРА
1. Турчак Л.И., Плотников П.В. Основы численных методов. – М.: Физматлит, 2002.
2. Численные методы / Лапчик М.П., Рагулина М.И., Хеннер Е.К. М.: Издат. центр «Академия», 2004.
3. Приближенное решение нелинейных уравнений: Метод. указания / КХТИ. Сост. А.В. Садыков, Казань, 1991.
4. Некоторые методы решения задачи аппроксимации: Метод. указания / Казан. гос. технол. ун-т. Сост. А.Г. Багоутдинова, Т.А. Хрузина, Казань, 2000.
Вариант 5
1. Отделить корни уравнения графически и уточнить один из них методом итераций с точностью  =0,001.
=0,001.
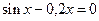
2. Решить систему нелинейных уравнений методом Ньютона с точностью  . Начальное приближение определить графическим способом.
. Начальное приближение определить графическим способом.
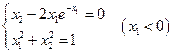
3. Решить систему линейных уравнений с трехдиагональной матрицей методом прогонки
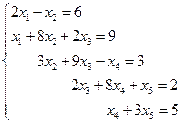
4. Решить систему линейных уравнений методом Зейделя с точностью  .
.
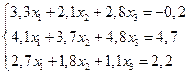
5. Функция задана таблично:

| 0,4 | 1,6 | 2,5 | ||

| -0,1 | 0,5 | 1,8 | 2,9 | 2,6 |
Построить интерполяционный полином Лагранжа для этой функции. С помощью этого полинома найти приближенное значение функции в точке 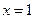 .
.
6. Построить интерполяционный полином Ньютона для функции, заданной таблично:

| 0,4 | 0,6 | 0,8 | 1,0 | 1,2 |

| 2,3 | 2,8 | 3,4 | 4,2 | 3,9 |
С помощью этого полинома найти приближенное значение функции при  .
.
7. Вычислить определенный интеграл методами прямоугольников, трапеций и парабол при 
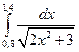
8. Функция задана таблично

| 2,5 | 3,5 | 4,1 | ||||

| 2,91 | 5,92 | 7,41 | 8,92 | 7,41 | 12,11 | 14,85 |
Построить аппроксимирующую прямую 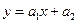 , используя метод наименьших квадратов (решить сначала вручную, затем с помощью программы).
, используя метод наименьших квадратов (решить сначала вручную, затем с помощью программы).
9. Дана задача Коши для обыкновенного дифференциального уравнения I порядка:
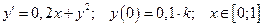 (
( – номер варианта)
– номер варианта)
Найти численное решение задачи методами Эйлера и Рунге-Кутта при  .
.
10. Найти численное решение краевой задачи
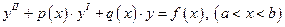
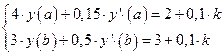
методом конечных разностей
а) вручную: при 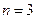 ;
;
б) с помощью программы: при  .
.
Здесь
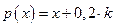 ;
; 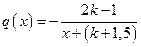 ;
; 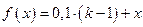
 ;
;  ;
;  – номер варианта
– номер варианта
ЛИТЕРАТУРА
1. Турчак Л.И., Плотников П.В. Основы численных методов. – М.: Физматлит, 2002.
2. Численные методы / Лапчик М.П., Рагулина М.И., Хеннер Е.К. М.: Издат. центр «Академия», 2004.
3. Приближенное решение нелинейных уравнений: Метод. указания / КХТИ. Сост. А.В. Садыков, Казань, 1991.
4. Некоторые методы решения задачи аппроксимации: Метод. указания / Казан. гос. технол. ун-т. Сост. А.Г. Багоутдинова, Т.А. Хрузина, Казань, 2000.
Вариант 6
1. Отделить корни уравнения графически и уточнить один из них методом касательных с точностью  =0,001.
=0,001.

2. Решить систему нелинейных уравнений методом Ньютона с точностью  . Начальное приближение определить графическим способом.
. Начальное приближение определить графическим способом.
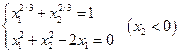
3. Решить систему линейных уравнений с трехдиагональной матрицей методом прогонки

4. Решить систему линейных уравнений методом Зейделя с точностью  .
.

5. Функция задана таблично:

| 0,6 | 1,5 | 2,1 | ||

| 0,9 | 1,4 | 2,6 | 3,2 | 2,9 |
Построить интерполяционный полином Лагранжа для этой функции. С помощью этого полинома найти приближенное значение функции в точке 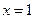 .
.
6. Построить интерполяционный полином Ньютона для функции, заданной таблично:

| 0,4 | 0,6 | 0,8 | 1,0 | 1,2 |

| 5,5 | 5,9 | 5,1 | 4,8 | 3,9 |
С помощью этого полинома найти приближенное значение функции при  .
.
7. Вычислить определенный интеграл методами прямоугольников, трапеций и парабол при 

8. Функция задана таблично

| 0,5 | 2,5 | 3,5 | ||||

| 1,21 | 2,15 | 4,21 | 5,12 | 6,11 | 7,15 | 8,21 |
Построить аппроксимирующую прямую 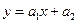 , используя метод наименьших квадратов (решить сначала вручную, затем с помощью программы).
, используя метод наименьших квадратов (решить сначала вручную, затем с помощью программы).
9. Дана задача Коши для обыкновенного дифференциального уравнения I порядка:
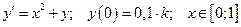 (
( – номер варианта)
– номер варианта)
Найти численное решение задачи методами Эйлера и Рунге-Кутта при  .
.
10. Найти численное решение краевой задачи
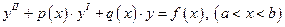
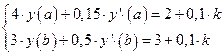
методом конечных разностей
а) вручную: при 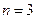 ;
;
б) с помощью программы: при  .
.
Здесь
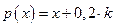 ;
; 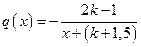 ;
; 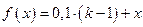
 ;
;  ;
;  – номер варианта
– номер варианта
ЛИТЕРАТУРА
1. Турчак Л.И., Плотников П.В. Основы численных методов. – М.: Физматлит, 2002.
2. Численные методы / Лапчик М.П., Рагулина М.И., Хеннер Е.К. М.: Издат. центр «Академия», 2004.
3. Приближенное решение нелинейных уравнений: Метод. указания / КХТИ. Сост. А.В. Садыков, Казань, 1991.
4. Некоторые методы решения задачи аппроксимации: Метод. указания / Казан. гос. технол. ун-т. Сост. А.Г. Багоутдинова, Т.А. Хрузина, Казань, 2000.
Вариант 7
1. Отделить корни уравнения графически и уточнить один из них методом итераций точностью  =0,001.
=0,001.
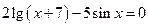
2. Решить систему нелинейных уравнений методом Ньютона с точностью  . Начальное приближение определить графическим способом.
. Начальное приближение определить графическим способом.
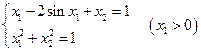
3. Решить систему линейных уравнений с трехдиагональной матрицей методом прогонки
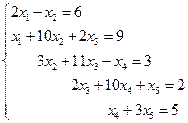
4. Решить систему линейных уравнений методом Зейделя с точностью  .
.

5. Функция задана таблично:

| 0,2 | 1,2 | 2,5 | ||

| 0,7 | 1,1 | 1,9 | 1,5 | 0,9 |
Построить интерполяционный полином Лагранжа для этой функции. С помощью этого полинома найти приближенное значение функции в точке 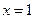 .
.
6. Построить интерполяционный полином Ньютона для функции, заданной таблично:

| 0,1 | 0,3 | 0,5 | 0,7 | 0,9 |

| 1,8 | 2,3 | 2,8 | 3,7 | 3,2 |
С помощью этого полинома найти приближенное значение функции при 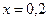 .
.
7. Вычислить определенный интеграл методами прямоугольников, трапеций и парабол при 
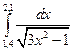
8. Функция задана таблично

| 0,5 | 1,5 | 2,5 | 4,5 | |||

| 1,31 | 3,28 | 4,25 | 5,31 | 6,29 | 8,26 | 9,21 |
Построить аппроксимирующую прямую 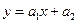 , используя метод наименьших квадратов (решить сначала вручную, затем с помощью программы).
, используя метод наименьших квадратов (решить сначала вручную, затем с помощью программы).
9. Дана задача Коши для обыкновенного дифференциального уравнения I порядка:
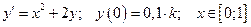 (
( – номер варианта)
– номер варианта)
Найти численное решение задачи методами Эйлера и Рунге-Кутта при  .
.
10. Найти численное решение краевой задачи
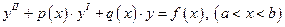
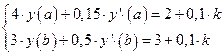
методом конечных разностей
а) вручную: при 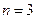 ;
;
б) с помощью программы: при  .
.
Здесь
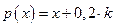 ;
; 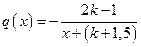 ;
; 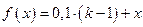
 ;
;  ;
;  – номер варианта
– номер варианта
ЛИТЕРАТУРА
1. Турчак Л.И., Плотников П.В. Основы численных методов. – М.: Физматлит, 2002.
2. Численные методы / Лапчик М.П., Рагулина М.И., Хеннер Е.К. М.: Издат. центр «Академия», 2004.
3. Приближенное решение нелинейных уравнений: Метод. указания / КХТИ. Сост. А.В. Садыков, Казань, 1991.
4. Некоторые методы решения задачи аппроксимации: Метод. указания / Казан. гос. технол. ун-т. Сост. А.Г. Багоутдинова, Т.А. Хрузина, Казань, 2000.
Вариант 8
1. Отделить корни уравнения графически и уточнить один из них методом касательных с точностью  =0,001.
=0,001.
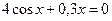
2. Решить систему нелинейных уравнений методом Ньютона с точностью  . Начальное приближение определить графическим способом.
. Начальное приближение определить графическим способом.

3. Решить систему линейных уравнений с трехдиагональной матрицей методом прогонки
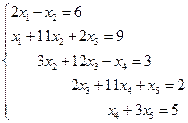
4. Решить систему линейных уравнений методом Зейделя с точностью  .
.
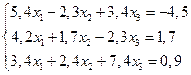
5. Функция задана таблично:

| 0,4 | 1,4 | 2,5 | ||

| 4,1 | 3,2 | 3,8 | 4,3 | 5,2 |
Построить интерполяционный полином Лагранжа для этой функции. С помощью этого полинома найти приближенное значение функции в точке 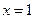 .
.
6. Построить интерполяционный полином Ньютона для функции, заданной таблично:

| 0,1 | 0,5 | 0,9 | 1,3 | 1,7 |

| 2,2 | 2,8 | 3,7 | 4,2 | 3,9 |
С помощью этого полинома найти приближенное значение функции при 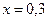 .
.
7. Вычислить определенный интеграл методами прямоугольников, трапеций и парабол при 
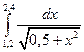
8. Функция задана таблично

| 1,5 | 4,5 | |||||

| 2,31 | 3,35 | 4,28 | 6,31 | 8,29 | 9,21 | 10,32 |
Построить аппроксимирующую прямую 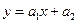 , используя метод наименьших квадратов (решить сначала вручную, затем с помощью программы).
, используя метод наименьших квадратов (решить сначала вручную, затем с помощью программы).
9. Дана задача Коши для обыкновенного дифференциального уравнения I порядка:
 (
( – номер варианта)
– номер варианта)
Найти численное решение задачи методами Эйлера и Рунге-Кутта при  .
.
10. Найти численное решение краевой задачи
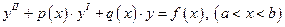
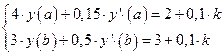
методом конечных разностей
а) вручную: при 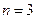 ;
;
б) с помощью программы: при  .
.
Здесь
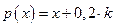 ;
; 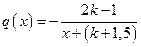 ;
; 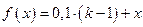
 ;
;  ;
;  – номер варианта
– номер варианта
ЛИТЕРАТУРА
1. Турчак Л.И., Плотников П.В. Основы численных методов. – М.: Физматлит, 2002.
2. Численные методы / Лапчик М.П., Рагулина М.И., Хеннер Е.К. М.: Издат. центр «Академия», 2004.
3. Приближенное решение нелинейных уравнений: Метод. указания / КХТИ. Сост. А.В. Садыков, Казань, 1991.
4. Некоторые методы решения задачи аппроксимации: Метод. указания / Казан. гос. технол. ун-т. Сост. А.Г. Багоутдинова, Т.А. Хрузина, Казань, 2000.
Вариант 9
1. Отделить корни уравнения графически и уточнить один из них методом итераций с точностью  =0,001.
=0,001.
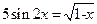
2. Решить систему нелинейных уравнений методом Ньютона с точностью  . Начальное приближение определить графическим способом.
. Начальное приближение определить графическим способом.

3. Решить систему линейных уравнений с трехдиагональной матрицей методом прогонки
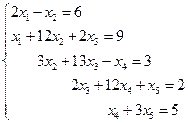
4. Решить систему линейных уравнений методом Зейделя с точностью  .
.
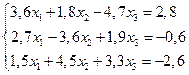
5. Функция задана таблично:

| 0,6 | 1,5 | 2,1 | ||

| -3 | -2,4 | 0,2 | 0,7 | 0,6 |
Построить интерполяционный полином Лагранжа для этой функции. С помощью этого полинома найти приближенное значение функции в точке 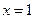 .
.
6. Построить интерполяционный полином Ньютона для функции, заданной таблично:

| 0,2 | 0,4 | 0,6 | 0,8 | 1,0 |

| 2,2 | 2,9 | 3,8 | 4,1 | 3,9 |
С помощью этого полинома найти приближенное значение функции при 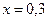 .
.
7. Вычислить определенный интеграл методами прямоугольников, трапеций и парабол при 
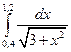
8. Функция задана таблично

| 0,5 | 1,4 | 2,5 | 3,4 | |||

| 1,61 | 4,31 | 6,02 | 7,58 | 9,08 | 10,25 | 12,19 |
Построить аппроксимирующую прямую 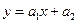 , используя метод наименьших квадратов (решить сначала вручную, затем с помощью программы).
, используя метод наименьших квадратов (решить сначала вручную, затем с помощью программы).
9. Дана задача Коши для обыкновенного дифференциального уравнения I порядка:
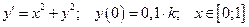 (
( – номер варианта)
– номер варианта)
Найти численное решение задачи методами Эйлера и Рунге-Кутта при  .
.
10. Найти численное решение краевой задачи
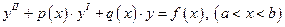
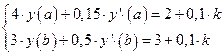
методом конечных разностей
а) вручную: при 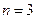 ;
;
б) с помощью программы: при  .
.
Здесь
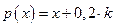 ;
; 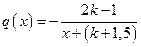 ;
; 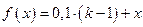
 ;
;  ;
;  – номер варианта
– номер варианта
ЛИТЕРАТУРА
1. Турчак Л.И., Плотников П.В. Основы численных методов. – М.: Физматлит, 2002.
2. Численные методы / Лапчик М.П., Рагулина М.И., Хеннер Е.К. М.: Издат. центр «Академия», 2004.
3. Приближенное решение нелинейных уравнений: Метод. указания / КХТИ. Сост. А.В. Садыков, Казань, 1991.
4. Некоторые методы решения задачи аппроксимации: Метод. указания / Казан. гос. технол. ун-т. Сост. А.Г. Багоутдинова, Т.А. Хрузина, Казань, 2000.
Вариант 10
1. Отделить корни уравнения графически и уточнить один из них методом касательных с точностью  =0,001.
=0,001.
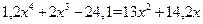
2. Решить систему нелинейных уравнений методом Ньютона с точностью  . Начальное приближение определить графическим способом.
. Начальное приближение определить графическим способом.

3. Решить систему линейных уравнений с трехдиагональной матрицей методом прогонки
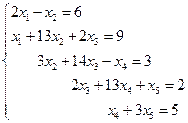
4. Решить систему линейных уравнений методом Зейделя с точностью  .
.
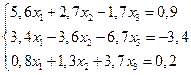
5. Функция задана таблично:

| 0,4 | 1,5 | |||

| 0,8 | 1,9 | 2,7 | 3,2 | 2,9 |
Построить интерполяционный полином Лагранжа для этой функции. С помощью этого полинома найти приближенное значение функции в точке 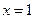 .
.
6. Построить интерполяционный полином Ньютона для функции, заданной таблично:

| 0,1 | 0,3 | 0,5 | 0,7 | 0,9 |

| 2,2 | 2,8 | 3,5 | 4,3 | 4,1 |
С помощью этого полинома найти приближенное значение функции при 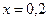 .
.
7. Вычислить определенный интеграл методами прямоугольников, трапеций и парабол при 
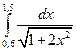
8. Функция задана таблично

| 1,2 | 2,1 | 2,5 | 3,5 | |||

| 2,5 | 4,3 | 5,1 | 6,1 | 7,2 | 8,15 | 10,1 |
Построить аппроксимирующую прямую 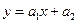 , используя метод наименьших квадратов (решить сначала вручную, затем с помощью программы).
, используя метод наименьших квадратов (решить сначала вручную, затем с помощью программы).
9. Дана задача Коши для обыкновенного дифференциального уравнения I порядка:
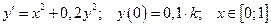 (
( – номер варианта)
– номер варианта)
Найти численное решение задачи методами Эйлера и Рунге-Кутта при  .
.
10. Найти численное решение краевой задачи
Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг
(0.163 сек.)