 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Линейная зависимость векторов. Векторы называются линейно зависимыми, если выполняются условия: и
Векторы  называются линейно зависимыми, если выполняются условия:
называются линейно зависимыми, если выполняются условия: 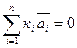 и
и  . В противном случае векторы
. В противном случае векторы  называются линейно независимыми. Максимальное число линейно независимых векторов образует базис векторного пространства.
называются линейно независимыми. Максимальное число линейно независимых векторов образует базис векторного пространства.
П р и м е р. Один базисный вектор определяет одномерное векторное пространство (числовая ось).
П р и м е р. Система из двух линейно независимых векторов определяет двумерное векторное пространство (плоскость) и т.д.
Геометрическую интерпретацию допускают векторные пространства, размерность которых не превышает трех.
Если векторы  образуют базис векторного пространства, то любой другой вектор
образуют базис векторного пространства, то любой другой вектор 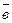 из этого пространства можно выразить через базисные векторы:
из этого пространства можно выразить через базисные векторы: 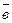 =
=  . При этом множители кi называются координатами вектора
. При этом множители кi называются координатами вектора 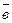 в базисе, образованным векторами
в базисе, образованным векторами  . Базис векторного пространства образован системой из одного, двух и трех единичных взаимно перпендикулярных векторов, называется декартовым.
. Базис векторного пространства образован системой из одного, двух и трех единичных взаимно перпендикулярных векторов, называется декартовым.
Декартов базис определяет известную из средней школы декартову прямоугольную систему координат. Единичные базисные векторы в декартовой системе координат называются ортами и обозначаются буквами i, j, k. Если вектор  задан координатами точек А и В: А(х 1, у 1, z 1), В(х 2, у 2, z 2), то координаты вектора
задан координатами точек А и В: А(х 1, у 1, z 1), В(х 2, у 2, z 2), то координаты вектора  будут следующими:
будут следующими:  (х 2- х 1, у 2- у 1, z 2- z 1). При этом вектор
(х 2- х 1, у 2- у 1, z 2- z 1). При этом вектор  можно представить:
можно представить:
 =(х 2- х 1) i +(y 2- y 1) j +(z 2- z 1) k.
=(х 2- х 1) i +(y 2- y 1) j +(z 2- z 1) k.
Если имеется равенство  , то говорят что вектор
, то говорят что вектор 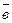 является линейной комбинации векторов
является линейной комбинации векторов  . При этом выполняется следующее свойство: координаты линейной комбинации векторов равны линейной комбинации соответствующих координат этих векторов.
. При этом выполняется следующее свойство: координаты линейной комбинации векторов равны линейной комбинации соответствующих координат этих векторов.
Определение. Проекцией вектора 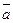 на ось l называется величина, определяемая соотношением:
на ось l называется величина, определяемая соотношением:  , где φ - угол между осью l и вектором
, где φ - угол между осью l и вектором 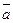 .
.
В декартовом прямоугольном базисе проекции вектора на оси координат можно отождествлять с координатами вектора в этом базисе.
Теорема. Если система некоторых векторов образует базис векторного пространства, то определитель, составленный из координат этих векторов, будет отличный от нуля.
Задача. Показать, что векторы 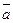 (3;5) и
(3;5) и 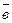 (-2;3) образуют базис векторного пространства и найти координаты вектора
(-2;3) образуют базис векторного пространства и найти координаты вектора  (4;13) в этом базисе.
(4;13) в этом базисе.
Решение:
Вычислим определитель, составленный из координат векторов 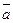 и
и 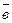 :
:  . Поскольку Δ≠0, следовательно, векторы
. Поскольку Δ≠0, следовательно, векторы 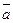 и
и 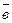 образуют базис векторного пространства. Тогда вектор
образуют базис векторного пространства. Тогда вектор  будет линейной комбинацией базисных векторов:
будет линейной комбинацией базисных векторов:  = к 1
= к 1 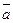 + к 2
+ к 2 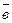 . Запишем это векторное равенство в координатной форме:
. Запишем это векторное равенство в координатной форме:

Решая систему линейных уравнений, получим: к 1=2; к 2=1. Следовательно,  или вектор
или вектор  имеет координаты 2 и 1 в базисе, образованном векторами
имеет координаты 2 и 1 в базисе, образованном векторами 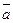 и
и 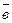 .
.
Ответ:  .
.
Поиск по сайту: