Решение систем линейных уравнений по формулам Крамера

Пусть имеется система n линейных уравнений с n неизвестными. Ее решение по формулам Крамера определяется следующим образом: 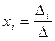, где D - определитель, составленный из коэффициентов при неизвестных, а D _i - определитель, который отличается от определителя D тем, что в нем столбец коэффициентов при переменной х_i заменяется столбцом свободных членов. Рассмотрим возможные варианты решений системы линейных уравнений по формулам Крамера.

а) Если определитель D¹0, система линейных уравнений будет совместной и определенной, т. е. имеет единственное решение, которое определяется по формулам Крамера.

П р и м е р. Решить систему линейных уравнений по формулам Крамера: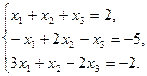

Решение:

Вычисляем определители D, D₁, D₂, D₃.

.

Поскольку D=-15¹0, система линейных уравнений имеет единственное решение.

;

;

.

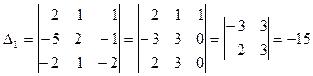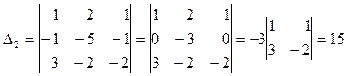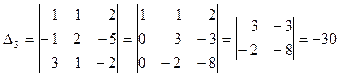Находим решение системы.

.

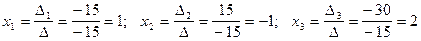Ответ: х₁ = 1; х₂ = -1; х₃ = 2.

б) Если определитель D будет равен нулю, а хотя бы один из определителей D _i ¹ 0, то в этом случае система будет несовместной, т. е. не имеет решения.

П р и м е р. Решить систему линейных уравнений по формулам Крамера:

Решение:

Вычисляем определители D и D _i:

, (этот результат можно было записать без вычислений, т. к. в определителе одинаковые первый и третий столбец.

.

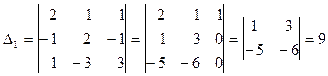Поскольку D=0, а D _i ¹0, следовательно, система не имеет решения.

Ответ. Решения система не имеет.

в) Если определитель D и все определители D _i будут равны нулю, то система, если она будет совместной, имеет множество решений.

П р и м е р. Решить систему линейных уравнений по формулам Крамера: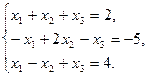

Решение:

Вычисляем определители D и D _i:

, т.к. первый и третий столбец в определителе одинаковые.

;

;

.

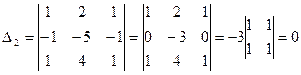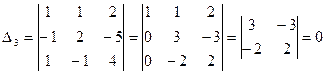Поскольку определители D и D _i равны нулю, то система линейных уравнений будет неопределенной (в случае ее совместности). В определителе D находим минор второго порядка, который будет отличный от нуля. Таким, например, будет минор .

Рассмотрим систему линейных уравнений, коэффициенты при неизвестных которой являются элементами минора М₃₃: 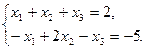В этой системе переменные х₁ и х₂ коэффициенты при которых являются элементами определителя М₃₃, будем считать основными, а переменная х₃ будет свободной, т. е. она может принимать любые значения.

Запишем систему двух линейных уравнений в виде:

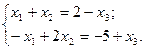
Решим систему по формулам Крамера:

;

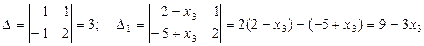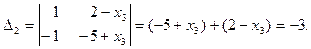
Найдем решение системы двух линейных уравнений с переменными х₁ и х₂.

; .

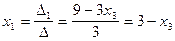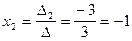Решение системы линейных уравнений, которое содержит свободные переменные, называется общим решением. Таким образом, х₁ =3- х₃; х₂ = -1 - общее решение системы линейных уравнений. Придавая свободным переменным произвольные значения, мы будем получать различные частные решения исходной системы. Например, при х₃ = 1, частное решение будет следующим: х₁ = 2; х₂ = -1; х₃ = 1; при х₃ = 2, частное решение будет таким: х₁ = 1; х₂ = -1; х₃ = 2. Таким образом, существует множество частных решений исходной системы.

Определение. Частное решение, которое определяется из общего решения системы линейных уравнений при условии, что свободные переменные будут равны нулю, называется базисным решением.

Исходная система линейных уравнений будет иметь следующее базисное решение: х₁ = 3; х₂ = -1; х₃ = 0. Проверка показывает, что это решение удовлетворяет всем трем уравнениям исходной системы, т. е. является ее решением.

Ответ: Система имеет множество решений.

Рассмотренная методика решения неопределенной системы линейных уравнений используется и в случае, если число переменных изначально превышает число уравнений.

Поиск по сайту: